2017年湖南省株洲市中考数学试卷
试卷更新日期:2017-07-18 类型:中考真卷
一、选择题
-
1. 计算a2•a4的结果为( )A、a2 B、a4 C、a6 D、a82. 如图示,数轴上点A所表示的数的绝对值为( )
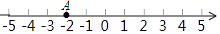 A、2 B、﹣2 C、±2 D、以上均不对3. 如图示直线l1 , l2△ABC被直线l3所截,且l1∥l2 , 则α=( )
A、2 B、﹣2 C、±2 D、以上均不对3. 如图示直线l1 , l2△ABC被直线l3所截,且l1∥l2 , 则α=( ) A、41° B、49° C、51° D、59°4. 已知实数a,b满足a+1>b+1,则下列选项错误的为( )A、a>b B、a+2>b+2 C、﹣a<﹣b D、2a>3b5. 如图,在△ABC中,∠BAC=x°,∠B=2x°,∠C=3x°,则∠BAD=( )
A、41° B、49° C、51° D、59°4. 已知实数a,b满足a+1>b+1,则下列选项错误的为( )A、a>b B、a+2>b+2 C、﹣a<﹣b D、2a>3b5. 如图,在△ABC中,∠BAC=x°,∠B=2x°,∠C=3x°,则∠BAD=( ) A、145° B、150° C、155° D、160°6. 下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )A、正三角形 B、正方形 C、正五边形 D、正六边形7. 株洲市展览馆某天四个时间段进出馆人数统计如下,则馆内人数变化最大时间段为( )
A、145° B、150° C、155° D、160°6. 下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )A、正三角形 B、正方形 C、正五边形 D、正六边形7. 株洲市展览馆某天四个时间段进出馆人数统计如下,则馆内人数变化最大时间段为( )9:00﹣10:00
10:00﹣11:00
14:00﹣15:00
15:00﹣16:00
进馆人数
50
24
55
32
出馆人数
30
65
28
45
A、9:00﹣10:00 B、10:00﹣11:00 C、14:00﹣15:00 D、15:00﹣16:008. 三名初三学生坐在仅有的三个座位上,起身后重新就坐,恰好有两名同学没有坐回原座位的概率为( )A、 B、 C、 D、9. 如图,点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的为( )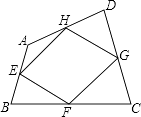 A、一定不是平行四边形 B、一定不是中心对称图形 C、可能是轴对称图形 D、当AC=BD时它是矩形10. 如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
A、一定不是平行四边形 B、一定不是中心对称图形 C、可能是轴对称图形 D、当AC=BD时它是矩形10. 如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( ) A、5 B、4 C、 D、
A、5 B、4 C、 D、二、填空题
-
11.
如图示在△ABC中∠B= .
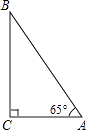 12. 分解因式:m3﹣mn2= .13. 分式方程 ﹣ =0的解为 .14. 已知“x的3倍大于5,且x的一半与1的差不大于2”,则x的取值范围是 .15. 如图,已知AM为⊙O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交⊙O于点D、E,∠BMD=40°,则∠EOM= .
12. 分解因式:m3﹣mn2= .13. 分式方程 ﹣ =0的解为 .14. 已知“x的3倍大于5,且x的一半与1的差不大于2”,则x的取值范围是 .15. 如图,已知AM为⊙O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交⊙O于点D、E,∠BMD=40°,则∠EOM= .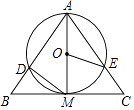 16.
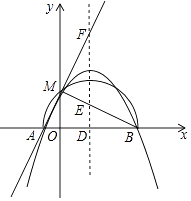
16.如图示直线y= x+ 与x轴、y轴分别交于点A、B,当直线绕着点A按顺时针方向旋转到与x轴首次重合时,点B运动的路径的长度为 .
 17. 如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1= (x>0)的图象上,顶点B在函数y2= (x>0)的图象上,∠ABO=30°,则 = .
17. 如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1= (x>0)的图象上,顶点B在函数y2= (x>0)的图象上,∠ABO=30°,则 = .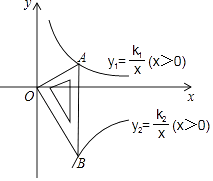 18. 如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(﹣1,0)与点C(x2 , 0),且与y轴交于点B(0,﹣2),小强得到以下结论:①0<a<2;②﹣1<b<0;③c=﹣1;④当|a|=|b|时x2> ﹣1;以上结论中正确结论的序号为 .
18. 如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(﹣1,0)与点C(x2 , 0),且与y轴交于点B(0,﹣2),小强得到以下结论:①0<a<2;②﹣1<b<0;③c=﹣1;④当|a|=|b|时x2> ﹣1;以上结论中正确结论的序号为 .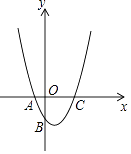
三、解答题
-
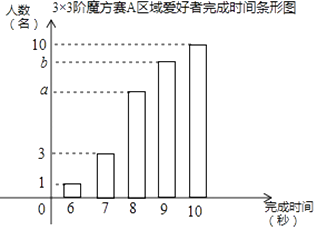
19. 计算: +20170×(﹣1)﹣4sin45°.20. 化简求值:(x﹣ )• ﹣y,其中x=2,y= .21. 某次世界魔方大赛吸引世界各地共600名魔方爱好者参加,本次大赛首轮进行3×3阶魔方赛,组委会随机将爱好者平均分到20个区域,每个区域30名同时进行比赛,完成时间小于8秒的爱好者进入下一轮角逐;如图是3×3阶魔方赛A区域30名爱好者完成时间统计图,求:
①A区域3×3阶魔方爱好者进入下一轮角逐的人数的比例(结果用最简分数表示).
②若3×3阶魔方赛各个区域的情况大体一致,则根据A区域的统计结果估计在3×3阶魔方赛后进入下一轮角逐的人数.
③若3×3阶魔方赛A区域爱好者完成时间的平均值为8.8秒,求该项目赛该区域完成时间为8秒的爱好者的概率(结果用最简分数表示).
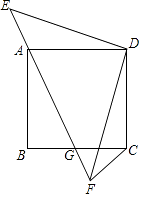
 22. 如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
22. 如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG.
 23.
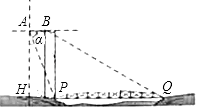
23.如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的俯角为α其中tanα=2 ,无人机的飞行高度AH为500 米,桥的长度为1255米.
①求点H到桥左端点P的距离;
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.
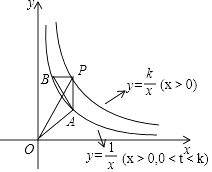
 24. 如图所示,Rt△PAB的直角顶点P(3,4)在函数y= (x>0)的图象上,顶点A、B在函数y= (x>0,0<t<k)的图象上,PA∥y轴,连接OP,OA,记△OPA的面积为S△OPA , △PAB的面积为S△PAB , 设w=S△OPA﹣S△PAB .
24. 如图所示,Rt△PAB的直角顶点P(3,4)在函数y= (x>0)的图象上,顶点A、B在函数y= (x>0,0<t<k)的图象上,PA∥y轴,连接OP,OA,记△OPA的面积为S△OPA , △PAB的面积为S△PAB , 设w=S△OPA﹣S△PAB .①求k的值以及w关于t的表达式;
②若用wmax和wmin分别表示函数w的最大值和最小值,令T=wmax+a2﹣a,其中a为实数,求Tmin .
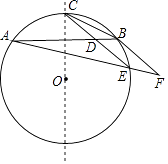
 25. 如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.
25. 如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.①求证:CE∥BF;
②若BD=2,且EA:EB:EC=3:1: , 求△BCD的面积(注:根据圆的对称性可知OC⊥AB).
 26.
26.已知二次函数y=﹣x2+bx+c+1,
①当b=1时,求这个二次函数的对称轴的方程;
②若c=- b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
③若二次函数的图象与x轴交于点A(x1 , 0),B(x2 , 0),且x1<x2 , 与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足 = ,求二次函数的表达式.