2017年湖北省恩施州中考数学试卷

试卷更新日期：2017-07-18 类型：中考真卷

进入出卷网下载

一、选择题

1. 7的绝对值是（）

A、﹣7 B、7 C、 $\frac{1}{7}$ D、 $- \frac{1}{7}$

查看试题解析
2. 大美山水“硒都•恩施”是一张亮丽的名片，八方游客慕名而来，今年“五•一”期间，恩施州共接待游客1450000人，将1450000用科学记数法表示为（）

A、0.145×10⁶ B、14.5×10⁵ C、1.45×10⁵ D、1.45×10⁶

查看试题解析
3. 下列计算正确的是（）

A、a（a﹣1）=a²﹣a B、（a⁴）³=a⁷ C、a⁴+a³=a⁷ D、2a⁵÷a³=a²

查看试题解析
4. 下列图标是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 小明和他的爸爸妈妈共3人站成一排拍照，他的爸爸妈妈相邻的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
6. 如图，若∠A+∠ABC=180°，则下列结论正确的是（）

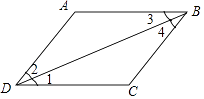A、∠1=∠2 B、∠2=∠3 C、∠1=∠3 D、∠2=∠4

查看试题解析
7. 函数y= $\frac{1}{x - 3}$ + $\sqrt{x - 1}$ 的自变量x的取值范围是（）

A、x≥1 B、x≥1且x≠3 C、x≠3 D、1≤x≤3

查看试题解析
8. 关于x的不等式组 ${\begin{matrix} x - m < 0 \\ 3 x - 1 > 2 (x - 1) \end{matrix}$ 无解，那么m的取值范围为（）

A、m≤﹣1 B、m＜﹣1 C、﹣1＜m≤0 D、﹣1≤m＜0

查看试题解析
9.
中国讲究五谷丰登，六畜兴旺，如图是一个正方体展开图，图中的六个正方形内分别标有六畜：“猪”、“牛”、“羊”、“马”、“鸡”、“狗”．将其围成一个正方体后，则与“牛”相对的是（）

A、羊 B、马 C、鸡 D、狗

查看试题解析
10. 某服装进货价80元/件，标价为200元/件，商店将此服装打x折销售后仍获利50%，则x为（）

A、5 B、6 C、7 D、8

查看试题解析
11. 如图，在△ABC中，DE∥BC，∠ADE=∠EFC，AD：BD=5：3，CF=6，则DE的长为（）

A、6 B、8 C、10 D、12

查看试题解析
12.
如图，在平面直角坐标系中2条直线为l₁：y=﹣3x+3，l₂：y=﹣3x+9，直线l₁交x轴于点A，交y轴于点B，直线l₂交x轴于点D，过点B作x轴的平行线交l₂于点C，点A、E关于y轴对称，抛物线y=ax²+bx+c过E、B、C三点，下列判断中：
①a﹣b+c=0；②2a+b+c=5；③抛物线关于直线x=1对称；④抛物线过点（b，c）；⑤S_四边形_ABCD=5，
其中正确的个数有（）

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

13. 16的平方根是．

查看试题解析
14. 分解因式：3ax²﹣6axy+3ay²= ．

查看试题解析
15. 如图，在Rt△ABC中，∠BAC=30°，以直角边AB为直径作半圆交AC于点D，以AD为边作等边△ADE，延长ED交BC于点F，BC=2 $\sqrt{3}$ ，则图中阴影部分的面积为．（结果不取近似值）

查看试题解析

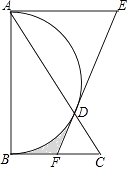
三、解答题

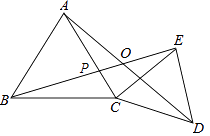
16. 先化简，再求值： $\frac{x - 2}{x^{2} + 2 x}$ ÷ $\frac{x^{2} - 4 x + 4}{x^{2} - 4}$ ﹣ $\frac{1}{2 x}$ ，其中x= $\sqrt{3}$ ．

查看试题解析
17. 如图，△ABC、△CDE均为等边三角形，连接BE，AD交于点O，AC与BE交于点P．求证：∠AOB=60°．

查看试题解析
18. 某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动，每位同学必须且只能选择一项球类运动，对该校学生随机抽取10%进行调查，根据调查结果绘制了如下不完整的频数分布表和扇形统计图：
运动项目
频数（人数）
羽毛球
30
篮球
a
乒乓球
36
排球
b
足球
12
请根据以上图表信息解答下列问题：

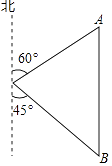
(1)、频数分布表中的a= ， b=；

(2)、在扇形统计图中，“排球”所在的扇形的圆心角为度；

(3)、全校有多少名学生选择参加乒乓球运动？

查看试题解析
19.
如图，小明家在学校O的北偏东60°方向，距离学校80米的A处，小华家在学校O的南偏东45°方向的B处，小华家在小明家的正南方向，求小华家到学校的距离．（结果精确到1米，参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73， $\sqrt{6}$ ≈2.45）

查看试题解析
20. 如图，∠AOB=90°，反比例函数y=﹣ $\frac{2}{x}$ （x＜0）的图象过点A（﹣1，a），反比例函数y= $\frac{k}{x}$ （k＞0，x＞0）的图象过点B，且AB∥x轴．

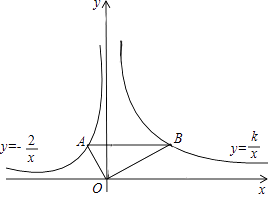(1)、求a和k的值；

(2)、过点B作MN∥OA，交x轴于点M，交y轴于点N，交双曲线y= $\frac{k}{x}$ 于另一点，求△OBC的面积．

查看试题解析
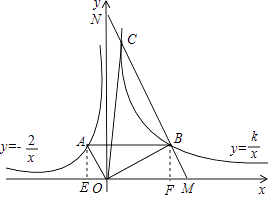21. 为积极响应政府提出的“绿色发展•低碳出行”号召，某社区决定购置一批共享单车．经市场调查得知，购买3辆男式单车与4辆女式单车费用相同，购买5辆男式单车与4辆女式单车共需16000元．

(1)、求男式单车和女式单车的单价；

(2)、该社区要求男式单比女式单车多4辆，两种单车至少需要22辆，购置两种单车的费用不超过50000元，该社区有几种购置方案？怎样购置才能使所需总费用最低，最低费用是多少？

查看试题解析
22. 如图，AB、CD是⊙O的直径，BE是⊙O的弦，且BE∥CD，过点C的切线与EB的延长线交于点P，连接BC．

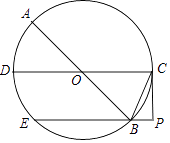(1)、求证：BC平分∠ABP；

(2)、求证：PC²=PB•PE；

(3)、若BE﹣BP=PC=4，求⊙O的半径．

查看试题解析
23.
如图，已知抛物线y=ax²+c过点（﹣2，2），（4，5），过定点F（0，2）的直线l：y=kx+2与抛物线交于A、B两点，点B在点A的右侧，过点B作x轴的垂线，垂足为C．

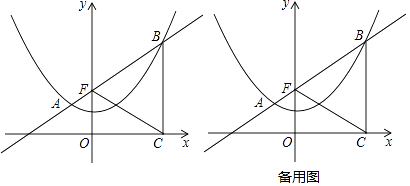(1)、求抛物线的解析式；

(2)、当点B在抛物线上运动时，判断线段BF与BC的数量关系（＞、＜、=），并证明你的判断；

(3)、P为y轴上一点，以B、C、F、P为顶点的四边形是菱形，设点P（0，m），求自然数m的值；

(4)、若k=1，在直线l下方的抛物线上是否存在点Q，使得△QBF的面积最大？若存在，求出点Q的坐标及△QBF的最大面积；若不存在，请说明理由．

查看试题解析

运动项目	频数（人数）
羽毛球	30
篮球	a
乒乓球	36
排球	b
足球	12