2017年山东省潍坊市中考数学试卷
试卷更新日期:2017-07-18 类型:中考真卷
一、选择题
-
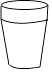
1. 下列算式,正确的是( )A、a3×a2=a6 B、a3÷a=a3 C、a2+a2=a4 D、(a2)2=a42. 如图所示的几何体,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 可燃冰,学名叫“天然气水合物”,是一种高效清洁、储量巨大的新能源.据报道,仅我国可燃冰预测远景资源量就超过了1000亿吨油当量.将1000亿用科学记数法可表示为( )A、1×103 B、1000×108 C、1×1011 D、1×10144.
3. 可燃冰,学名叫“天然气水合物”,是一种高效清洁、储量巨大的新能源.据报道,仅我国可燃冰预测远景资源量就超过了1000亿吨油当量.将1000亿用科学记数法可表示为( )A、1×103 B、1000×108 C、1×1011 D、1×10144.小莹和小博士下棋,小莹执圆子,小博士执方子.如图,棋盘中心方子的位置用(﹣1,0)表示,右下角方子的位置用(0,﹣1)表示.小莹将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形.他放的位置是( )
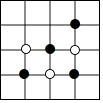 A、(﹣2,1) B、(﹣1,1) C、(1,﹣2) D、(﹣1,﹣2)5. 用教材中的计算器依次按键如下,显示的结果在数轴上对应点的位置介于( )之间.
A、(﹣2,1) B、(﹣1,1) C、(1,﹣2) D、(﹣1,﹣2)5. 用教材中的计算器依次按键如下,显示的结果在数轴上对应点的位置介于( )之间.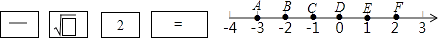 A、B与C B、C与D C、E与F D、A与B6. 如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )
A、B与C B、C与D C、E与F D、A与B6. 如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( )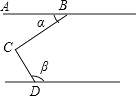 A、∠α+∠β=180° B、∠β﹣∠α=90° C、∠β=3∠α D、∠α+∠β=90°7. 甲、乙、丙、丁四名射击运动员在选选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示.丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )
A、∠α+∠β=180° B、∠β﹣∠α=90° C、∠β=3∠α D、∠α+∠β=90°7. 甲、乙、丙、丁四名射击运动员在选选拔赛中,每人射击了10次,甲、乙两人的成绩如表所示.丙、丁两人的成绩如图所示.欲选一名运动员参赛,从平均数与方差两个因素分析,应选( )甲
乙
平均数
9
8
方差
1
1
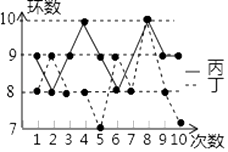 A、甲 B、乙 C、丙 D、丁8. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、
A、甲 B、乙 C、丙 D、丁8. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、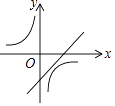 B、
B、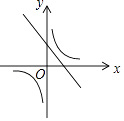 C、
C、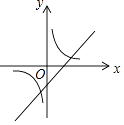 D、
D、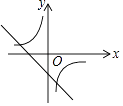 9. 若代数式 有意义,则实数x的取值范围是( )A、x≥1 B、x≥2 C、x>1 D、x>210. 如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )
9. 若代数式 有意义,则实数x的取值范围是( )A、x≥1 B、x≥2 C、x>1 D、x>210. 如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( ) A、50° B、60° C、80° D、90°11.
A、50° B、60° C、80° D、90°11.定义[x]表示不超过实数x的最大整数,如[1.8]=1,[﹣1.4]=﹣2,[﹣3]=﹣3.函数y=[x]的图象如图所示,则方程[x]= x2的解为( )#N.
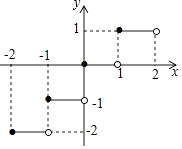 A、0或 B、0或2 C、1或 D、 或﹣12. 点A、C为半径是3的圆周上两点,点B为
A、0或 B、0或2 C、1或 D、 或﹣12. 点A、C为半径是3的圆周上两点,点B为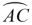 的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为( )
的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆直径的三等分点上,则该菱形的边长为( )
A、 或2 B、 或2 C、 或2 D、 或2二、填空题
-
13. 计算:(1﹣ )÷ = .14. 因式分解:x2﹣2x+(x﹣2)= .15. 如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: , 可以使得△FDB与△ADE相似.(只需写出一个)
 16. 若关于x的一元二次方程kx2﹣2x+1=0有实数根,则k的取值范围是 .17. 如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第n个图中正方形和等边三角形的个数之和为个.
16. 若关于x的一元二次方程kx2﹣2x+1=0有实数根,则k的取值范围是 .17. 如图,自左至右,第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;…按照此规律,第n个图中正方形和等边三角形的个数之和为个. 18. 如图,将一张矩形纸片ABCD的边BC斜着向AD边对折,使点B落在AD边上,记为B′,折痕为CE,再将CD边斜向下对折,使点D落在B′C边上,记为D′,折痕为CG,B′D′=2,BE= BC.则矩形纸片ABCD的面积为 .
18. 如图,将一张矩形纸片ABCD的边BC斜着向AD边对折,使点B落在AD边上,记为B′,折痕为CE,再将CD边斜向下对折,使点D落在B′C边上,记为D′,折痕为CG,B′D′=2,BE= BC.则矩形纸片ABCD的面积为 .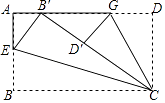
三、解答题
-
19. 本校为了解九年级男同学的体育考试准备情况,随机抽取部分男同学进行了1000米跑步测试.按照成绩分为优秀、良好、合格与不合格四个等级,学校绘制了如下不完整的统计图.
 (1)、根据给出的信息,补全两幅统计图;(2)、该校九年级有600名男生,请估计成绩未达到良好有多少名?(3)、某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米比赛.预赛分别为A、B、C三组进行,选手由抽签确定分组.甲、乙两人恰好分在同一组的概率是多少?20.
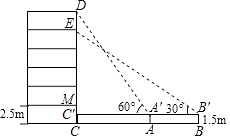
(1)、根据给出的信息,补全两幅统计图;(2)、该校九年级有600名男生,请估计成绩未达到良好有多少名?(3)、某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米比赛.预赛分别为A、B、C三组进行,选手由抽签确定分组.甲、乙两人恰好分在同一组的概率是多少?20.如图,某数学兴趣小组要测量一栋五层居民楼CD的高度.该楼底层为车库,高2.5米;上面五层居住,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶点E的仰角为30°,AB=14米.求居民楼的高度(精确到0.1米,参考数据: ≈1.73)
 21. 某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨.第一批蒜薹价格为4000元/吨;因蒜薹大量上市,第二批价格跌至1000元/吨.这两批蒜苔共用去16万元.(1)、求两批次购进蒜薹各多少吨?(2)、公司收购后对蒜薹进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润1000元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?22. 如图,AB为半圆O的直径,AC是⊙O的一条弦,D为 的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
21. 某蔬菜加工公司先后两批次收购蒜薹(tái)共100吨.第一批蒜薹价格为4000元/吨;因蒜薹大量上市,第二批价格跌至1000元/吨.这两批蒜苔共用去16万元.(1)、求两批次购进蒜薹各多少吨?(2)、公司收购后对蒜薹进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润1000元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?22. 如图,AB为半圆O的直径,AC是⊙O的一条弦,D为 的中点,作DE⊥AC,交AB的延长线于点F,连接DA. (1)、求证:EF为半圆O的切线;(2)、若DA=DF=6 ,求阴影区域的面积.(结果保留根号和π)23. 工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)
(1)、求证:EF为半圆O的切线;(2)、若DA=DF=6 ,求阴影区域的面积.(结果保留根号和π)23. 工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计) (1)、在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?(2)、若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?24.
(1)、在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?(2)、若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?24.边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2
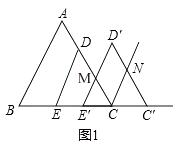 (1)、如图1,将△DEC沿射线方向平移,得到△D′E′C′,边D′E′与AC的交点为M,边C′D′与∠ACC′的角平分线交于点N,当CC′多大时,四边形MCND′为菱形?并说明理由.(2)、
(1)、如图1,将△DEC沿射线方向平移,得到△D′E′C′,边D′E′与AC的交点为M,边C′D′与∠ACC′的角平分线交于点N,当CC′多大时,四边形MCND′为菱形?并说明理由.(2)、如图2,将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD′、BE′.边D′E′的中点为P.
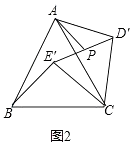
①在旋转过程中,AD′和BE′有怎样的数量关系?并说明理由;
②连接AP,当AP最大时,求AD′的值.(结果保留根号)
25.如图1,抛物线y=ax2+bx+c经过平行四边形ABCD的顶点A(0,3)、B(﹣1,0)、D(2,3),抛物线与x轴的另一交点为E.经过点E的直线l将平行四边形ABCD分割为面积相等两部分,与抛物线交于另一点F.点P在直线l上方抛物线上一动点,设点P的横坐标为t
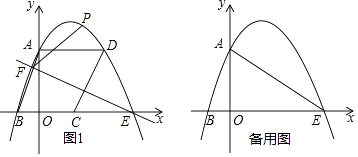 (1)、求抛物线的解析式;(2)、当t何值时,△PFE的面积最大?并求最大值的立方根;(3)、是否存在点P使△PAE为直角三角形?若存在,求出t的值;若不存在,说明理由.
(1)、求抛物线的解析式;(2)、当t何值时,△PFE的面积最大?并求最大值的立方根;(3)、是否存在点P使△PAE为直角三角形?若存在,求出t的值;若不存在,说明理由.