2017年湖南省长沙市中考数学试卷

试卷更新日期：2017-07-18 类型：中考真卷

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分）

1. 下列实数中，为有理数的是（）

A、 $\sqrt{3}$ B、π C、 $\sqrt[3]{2}$ D、1

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、a+2a=2a² C、x（1+y）=x+xy D、（mn²）³=mn⁶

查看试题解析
3. 据国家旅游局统计，2017年端午小长假全国各大景点共接待游客约为82600000人次，数据82600000用科学记数法表示为（）

A、0.826×10⁶ B、8.26×10⁷ C、82.6×10⁶ D、8.26×10⁸

查看试题解析
4. 在下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、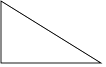直角三角形 B、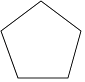正五边形 C、正方形 D、平行四边形

查看试题解析
5. 一个三角形的三个内角的度数之比为1：2：3，则这个三角形一定是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰直角三角形

查看试题解析
6. 下列说法正确的是（）

A、检测某批次灯泡的使用寿命，适宜用全面调查 B、可能性是1%的事件在一次试验中一定不会发生 C、数据3，5，4，1，﹣2的中位数是4 D、“367中有2人同月同日初生”为必然事件

查看试题解析
7. 某几何体的三视图如图所示，因此几何体是（）

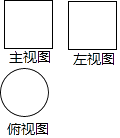A、长方形 B、圆柱 C、球 D、正三棱柱

查看试题解析
8. 抛物线y=2（x﹣3）²+4顶点坐标是（）

A、（3，4） B、（﹣3，4） C、（3，﹣4） D、（2，4）

查看试题解析
9. 如图，已知直线a∥b，直线c分别与a，b相交，∠1=110°，则∠2的度数为（）

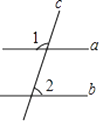A、60° B、70° C、80° D、110°

查看试题解析
10. 如图，菱形ABCD的对角线AC，BD的长分别为6cm，8cm，则这个菱形的周长为（）

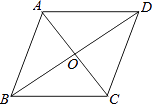A、5cm B、10cm C、14cm D、20cm

查看试题解析
11. 中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关，初日健步不为难，次日脚痛减一半，六朝才得到其关．”其大意是，有人要去某关口，路程为378里，第一天健步行走，从第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了六天才到达目的地，则此人第六天走的路程为（）

A、24里 B、12里 C、6里 D、3里

查看试题解析
12. 如图，将正方形ABCD折叠，使顶点A与CD边上的一点H重合（H不与端点C，D重合），折痕交AD于点E，交BC于点F，边AB折叠后与边BC交于点G．设正方形ABCD的周长为m，△CHG的周长为n，则 $\frac{n}{m}$ 的值为（）

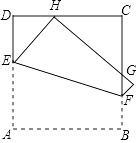A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{5} - 1}{2}$ D、随H点位置的变化而变化

查看试题解析

二、填空题

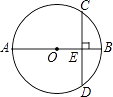
13. 分解因式：2a²+4a+2= ．

查看试题解析
14. 方程组 ${\begin{matrix} x + y = 1 \\ 3 x - y = 3 \end{matrix}$ 的解是．

查看试题解析
15. 如图，AB为⊙O的直径，弦CD⊥AB于点E，已知CD=6，EB=1，则⊙O的半径为．

查看试题解析
16. 如图，△ABO三个顶点的坐标分别为A（2，4），B（6，0），O（0，0），以原点O为位似中心，把这个三角形缩小为原来的 $\frac{1}{2}$ ，可以得到△A′B′O，已知点B′的坐标是（3，0），则点A′的坐标是．

查看试题解析
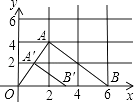17. 甲、乙两名同学进行跳高测试，每人10次跳高的平均成绩恰好是1.6米，方差分别是S_甲²=1.2，S_乙²=0.5，则在本次测试中，同学的成绩更稳定（填“甲”或“乙”）

查看试题解析
18. 如图，点M是函数y= $\sqrt{3}$ x与y= $\frac{k}{x}$ 的图象在第一象限内的交点，OM=4，则k的值为．

查看试题解析

三、解答题

19. 计算：|﹣3|+（π﹣2017）⁰﹣2sin30°+（ $\frac{1}{3}$ ）^﹣¹ ．

查看试题解析
20. 解不等式组 ${\begin{matrix} 2 x \geq - 9 - x \\ 5 x - 1 > 3 (x + 1) \end{matrix}$ ，并把它的解集在数轴上表示出来．

查看试题解析
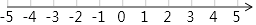21. 为了传承中华优秀传统文化，市教育局决定开展“经典诵读进校园”活动，某校团委组织八年级100名学生进行“经典诵读”选拔赛，赛后对全体参赛学生的成绩进行整理，得到下列不完整的统计图表．
组别
分数段
频次
频率
A
60≤x＜70
17
0.17
B
70≤x＜80
30
a
C
80≤x＜90
b
0.45
D
90≤x＜100
8
0.08
请根据所给信息，解答以下问题：

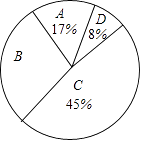(1)、表中a= ， b=；

(2)、请计算扇形统计图中B组对应扇形的圆心角的度数；

(3)、已知有四名同学均取得98分的最好成绩，其中包括来自同一班级的甲、乙两名同学，学校将从这四名同学中随机选出两名参加市级比赛，请用列表法或画树状图法求甲、乙两名同学都被选中的概率．

查看试题解析
22.
为了维护国家主权和海洋权利，海监部门对我国领海实现了常态化巡航管理，如图，正在执行巡航任务的海监船以每小时50海里的速度向正东方航行，在A处测得灯塔P在北偏东60°方向上，继续航行1小时到达B处，此时测得灯塔P在北偏东30°方向上．

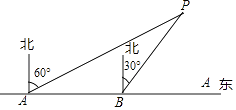(1)、求∠APB的度数；

(2)、已知在灯塔P的周围25海里内有暗礁，问海监船继续向正东方向航行是否安全？

查看试题解析
23. 如图，AB与⊙O相切于点C，OA，OB分别交⊙O于点D，E， $\hat{C D}$ = $\hat{C E}$

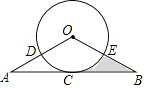(1)、求证：OA=OB；

(2)、已知AB=4 $\sqrt{3}$ ，OA=4，求阴影部分的面积．

查看试题解析
24. 自从湖南与欧洲的“湘欧快线”开通后，我省与欧洲各国经贸往来日益频繁，某欧洲客商准备在湖南采购一批特色商品，经调查，用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍，一件A型商品的进价比一件B型商品的进价多10元．

(1)、求一件A，B型商品的进价分别为多少元？

(2)、若该欧洲客商购进A，B型商品共250件进行试销，其中A型商品的件数不大于B型的件数，且不小于80件．已知A型商品的售价为240元/件，B型商品的售价为220元/件，且全部售出．设购进A型商品m件，求该客商销售这批商品的利润v与m之间的函数关系式，并写出m的取值范围；

(3)、在（2）的条件下，欧洲客商决定在试销活动中每售出一件A型商品，就从一件A型商品的利润中捐献慈善资金a元，求该客商售完所有商品并捐献慈善资金后获得的最大收益．

查看试题解析
25. 若三个非零实数x，y，z满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数x，y，z构成“和谐三组数”．

(1)、实数1，2，3可以构成“和谐三组数”吗？请说明理由；

(2)、若M（t，y₁），N（t+1，y₂），R（t+3，y₃）三点均在函数 $\frac{k}{x}$ （k为常数，k≠0）的图象上，且这三点的纵坐标y₁ ， y₂ ， y₃构成“和谐三组数”，求实数t的值；

(3)、若直线y=2bx+2c（bc≠0）与x轴交于点A（x₁ ， 0），与抛物线y=ax²+3bx+3c（a≠0）交于B（x₂ ， y₂），C（x₃ ， y₃）两点．
①求证：A，B，C三点的横坐标x₁ ， x₂ ， x₃构成“和谐三组数”；
②若a＞2b＞3c，x₂=1，求点P（ $\frac{c}{a}$ ， $\frac{b}{a}$ ）与原点O的距离OP的取值范围．

查看试题解析
26.
如图，抛物线y=mx²﹣16mx+48m（m＞0）与x轴交于A，B两点（点B在点A左侧），与y轴交于点C，点D是抛物线上的一个动点，且位于第四象限，连接OD、BD、AC、AD，延长AD交y轴于点E．

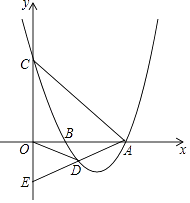(1)、若△OAC为等腰直角三角形，求m的值；

(2)、若对任意m＞0，C、E两点总关于原点对称，求点D的坐标（用含m的式子表示）；

(3)、当点D运动到某一位置时，恰好使得∠ODB=∠OAD，且点D为线段AE的中点，此时对于该抛物线上任意一点P（x₀ ， y₀）总有n+ $\frac{1}{6}$ ≥﹣4 $\sqrt{3}$ my₀²﹣12 $\sqrt{3}$ y₀﹣50成立，求实数n的最小值．

查看试题解析

组别	分数段	频次	频率
A	60≤x＜70	17	0.17
B	70≤x＜80	30	a
C	80≤x＜90	b	0.45
D	90≤x＜100	8	0.08