2017年湖南省常德市中考数学试卷

试卷更新日期：2017-07-17 类型：中考真卷

进入出卷网下载

一、选择题

1. 下列各数中无理数为（）

A、 $\sqrt{2}$ B、0 C、 $\frac{1}{2017}$ D、﹣1

查看试题解析
2. 若一个角为75°，则它的余角的度数为（）

A、285° B、105° C、75° D、15°

查看试题解析
3. 一元二次方程3x²﹣4x+1=0的根的情况为（）

A、没有实数根 B、只有一个实数根 C、两个相等的实数根 D、两个不相等的实数根

查看试题解析
4. 如图是根据我市某天七个整点时的气温绘制成的统计图，则这七个整点时气温的中位数和平均数分别是（）

A、30，28 B、26，26 C、31，30 D、26，22

查看试题解析
5. 下列各式由左到右的变形中，属于分解因式的是（）

A、a（m+n）=am+an B、a²﹣b²﹣c²=（a﹣b）（a+b）﹣c² C、10x²﹣5x=5x（2x﹣1） D、x²﹣16+6x=（x+4）（x﹣4）+6x

查看试题解析
6. 如图是一个几何体的三视图，则这个几何体是（）

A、 B、 C、 D、

查看试题解析
7. 将抛物线y=2x²向右平移3个单位，再向下平移5个单位，得到的抛物线的表达式为（）

A、y=2（x﹣3）²﹣5 B、y=2（x+3）²+5 C、y=2（x﹣3）²+5 D、y=2（x+3）²﹣5

查看试题解析
8. 如表是一个4×4（4行4列共16个“数”组成）的奇妙方阵，从这个方阵中选四个“数”，而且这四个“数”中的任何两个不在同一行，也不在同一列，有很多选法，把每次选出的四个“数”相加，其和是定值，则方阵中第三行三列的“数”是（）
3⁰
$\sqrt{4}$
2 $\sqrt{3}$ sin60°
2²
﹣3
﹣2
﹣ $\sqrt{2}$ sin45°
0
|﹣5|
6

2³
（ $\frac{1}{3}$ ）^﹣¹
4
$\sqrt{25}$
（ $\frac{1}{6}$ ）^﹣¹

A、5 B、6 C、7 D、8

查看试题解析

二、填空题

9. 计算：|﹣2|﹣ $\sqrt[3]{8}$ = ．

查看试题解析
10. 分式方程 $\frac{2}{x}$ +1= $\frac{4}{x}$ 的解为．

查看试题解析
11. 据统计：我国微信用户数量已突破887000000人，将887000000用科学记数法表示为．

查看试题解析
12. 命题：“如果m是整数，那么它是有理数”，则它的逆命题为：．

查看试题解析
13. 彭山的枇杷大又甜，在今年5月18日“彭山枇杷节”期间，从山上5棵枇杷树上采摘到了200千克枇杷，请估计彭山近600棵枇杷树今年一共收获了枇杷千克．

查看试题解析
14. 如图，已知Rt△ABE中∠A=90°，∠B=60°，BE=10，D是线段AE上的一动点，过D作CD交BE于C，并使得∠CDE=30°，则CD长度的取值范围是．

查看试题解析
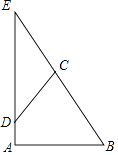15. 如图，正方形EFGH的顶点在边长为2的正方形的边上．若设AE=x，正方形EFGH的面积为y，则y与x的函数关系为．

查看试题解析
16.
如图，有一条折线A₁B₁A₂B₂A₃B₃A₄B₄…，它是由过A₁（0，0），B₁（2，2），A₂（4，0）组成的折线依次平移4，8，12，…个单位得到的，直线y=kx+2与此折线恰有2n（n≥1，且为整数）个交点，则k的值为．

查看试题解析

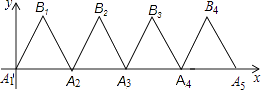
三、解答题

17. 甲、乙、丙三个同学站成一排进行毕业合影留念，请用列表法或树状图列出所有可能的情形，并求出甲、乙两人相邻的概率是多少？

查看试题解析
18. 求不等式组 ${\begin{matrix} \frac{4 (1 + x)}{3} - 1 \leq \frac{5 + x}{2} \dots ① \\ x - 5 \leq \frac{3}{2} (3 x - 2) \dots ② \end{matrix}$ 的整数解．

查看试题解析

四、解答题：

19. 先化简，再求值：（ $\frac{x^{2} - 4 x + 3}{x - 3}$ ﹣ $\frac{1}{3 - x}$ ）（ $\frac{x^{2} - 2 x + 1}{x^{2} - 3 x + 2}$ ﹣ $\frac{2}{x - 2}$ ），其中x=4．

查看试题解析
20. 在“一带一路”倡议下，我国已成为设施联通，贸易畅通的促进者，同时也带动了我国与沿线国家的货物交换的增速发展，如图是湘成物流园2016年通过“海、陆（汽车）、空、铁”四种模式运输货物的统计图．
请根据统计图解决下面的问题：

(1)、该物流园2016年货运总量是多少万吨？

(2)、该物流园2016年空运货物的总量是多少万吨？并补全条形统计图；

(3)、求条形统计图中陆运货物量对应的扇形圆心角的度数

查看试题解析

五、解答题：

21. 如图，已知反比例函数y= $\frac{k}{x}$ 的图象经过点A（4，m），AB⊥x轴，且△AOB的面积为2．

(1)、求k和m的值；

(2)、若点C（x，y）也在反比例函数y= $\frac{k}{x}$ 的图象上，当﹣3≤x≤﹣1时，求函数值y的取值范围．

查看试题解析
22. 如图，已知AB是⊙O的直径，CD与⊙O相切于C，BE∥CO．

(1)、求证：BC是∠ABE的平分线；

(2)、若DC=8，⊙O的半径OA=6，求CE的长．

查看试题解析

六、解答题：

23. 收发微信红包已成为各类人群进行交流联系，增强感情的一部分，下面是甜甜和她的双胞胎妹妹在六一儿童节期间的对话．
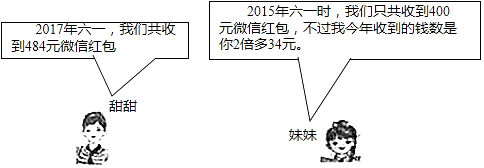
请问：

(1)、2015年到2017年甜甜和她妹妹在六一收到红包的年增长率是多少？

(2)、2017年六一甜甜和她妹妹各收到了多少钱的微信红包？

查看试题解析
24. 如图1，2分别是某款篮球架的实物图与示意图，已知底座BC=0.60米，底座BC与支架AC所成的角∠ACB=75°，支架AF的长为2.50米，篮板顶端F点到篮框D的距离FD=1.35米，篮板底部支架HE与支架AF所成的角∠FHE=60°，求篮框D到地面的距离（精确到0.01米）（参考数据：cos75°≈0.2588，sin75°≈0.9659，tan75°≈3.732， $\sqrt{3}$ ≈1.732， $\sqrt{2}$ ≈1.414）

查看试题解析

七、解答题：

25.
如图，已知抛物线的对称轴是y轴，且点（2，2），（1， $\frac{5}{4}$ ）在抛物线上，点P是抛物线上不与顶点N重合的一动点，过P作PA⊥x轴于A，PC⊥y轴于C，延长PC交抛物线于E，设M是O关于抛物线顶点N的对称点，D是C点关于N的对称点．

(1)、求抛物线的解析式及顶点N的坐标；

(2)、求证：四边形PMDA是平行四边形；

(3)、求证：△DPE∽△PAM，并求出当它们的相似比为 $\sqrt{3}$ 时的点P的坐标．

查看试题解析
26. 如图，直角△ABC中，∠BAC=90°，D在BC上，连接AD，作BF⊥AD分别交AD于E，AC于F．

(1)、如图1，若BD=BA，求证：△ABE≌△DBE；

(2)、如图2，若BD=4DC，取AB的中点G，连接CG交AD于M，
求证：①GM=2MC；
②AG²=AF•AC．

查看试题解析

3⁰	$\sqrt{4}$	2 $\sqrt{3}$ sin60°	2²
﹣3	﹣2	﹣ $\sqrt{2}$ sin45°	0
\|﹣5\|	6		2³
（ $\frac{1}{3}$ ）^﹣¹	4	$\sqrt{25}$	（ $\frac{1}{6}$ ）^﹣¹