甘肃省定西市陇西县五校2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2019-11-15 类型：期中考试

进入出卷网下载

一、单选题

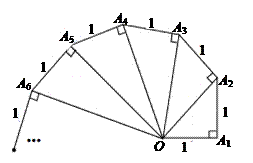
1. 25的算术平方根是（）

A、 $\pm 5$ B、 $5$ C、 $- 5$ D、 $\pm \sqrt{5}$

查看试题解析
2. 点P（3，﹣4）关于y轴的对称点P′的坐标是（）

A、（﹣3，﹣4） B、（3，4） C、（﹣3，4） D、（﹣4，3）

查看试题解析
3. 以下列各组数为三边的三角形中不是直角三角形的是（）

A、9、12、15 B、41、40、9 C、25、7、24 D、6、5、4

查看试题解析
4. 下列各数：3.141592 ， $- \sqrt{3}$ ，0.16， $\sqrt{0.01}$ ， $- π$ ， $0.1010010001 \dots \dots$ ， $\frac{22}{7}$ ， $\sqrt[3]{5}$ ， 0.2 ， $\sqrt{8}$ 中无理数的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 下列说法中，不正确的是

A、3是 ${(- 3)}^{2}$ 的算术平方根 B、－3是 ${(- 3)}^{2}$ 的算术平方根 C、±3是 ${(- 3)}^{2}$ 的平方根 D、－3是 ${(- 3)}^{3}$ 的立方根

查看试题解析
6. 已知一个直角三角形的两边分别是3和4，则第三边的平方是（）

A、25 B、7 C、25或7 D、5或 $\sqrt{7}$

查看试题解析
7. 点P(m+3，m+1)在直角坐标系的x轴上，则点P的坐标为（）

A、(0，﹣2) B、(2，0) C、(4，0) D、(0，﹣4)

查看试题解析
8. 下列函数中，y的值随x的值增大而增大的是（）

A、y= -3x B、y=2x - 1 C、y= -3x+10 D、y= -2x+1

查看试题解析
9. 已知 ${(x + 2)}^{2}$ + $\sqrt{y - 3}$ =0，则 $y^{x}$ 的值是（）

A、-6 B、 $\frac{1}{9}$ C、9 D、-8

查看试题解析
10. 下列根式是最简二次根式的是（）

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{0.3}$ C、 $\sqrt{3}$ D、 $\sqrt{20}$

查看试题解析
11. 下面哪个点不在函数y=-2x+3的图象上（）

A、 $(- 5 ， 13)$ B、 $(0.5 ， 2)$ C、 $(3 ， 0)$ D、 $(1 ， 1)$

查看试题解析
12. 若△ABC中，AB＝7，AC＝8，高AD＝6，则BC的长是（）

A、10+ $\sqrt{13}$ B、10－ $\sqrt{13}$ C、10+ $\sqrt{13}$ 或10－ $\sqrt{13}$ D、以上都不对

查看试题解析

二、填空题

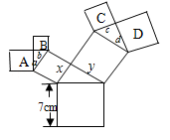
13. $\sqrt{3}$ -2的相反数是，绝对值是

查看试题解析
14. 如图所示图形中，所有的三角形都是直角三角形，所有的四边形都是正方形，其中最大的正方形边长为7cm.则正方形A、B、C、D的面积和是 ${cm}^{2}$ .

查看试题解析
15. 比较3 $\sqrt{2}$ 2 $\sqrt{3}$ ； $\frac{1}{2}$ $\frac{\sqrt{3} - 1}{2}$

查看试题解析
16. 平面直角坐标系内，点P（3，﹣4）到y轴的距离是.

查看试题解析
17. 如图，象棋盘上，若“将”位于点（0，-2），“车”位于点（-4，-2），则“马”位于点.

查看试题解析
18. 如图，一圆柱高8 cm，底面半径为 $\frac{6}{π}$ cm，一只蚂蚁从点 $A$ 爬到点 $B$ 处吃食，要爬行的最短路程是.

查看试题解析
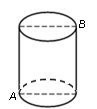19.
如图，已知OA=OB，那么数轴上点A所表示的数是

查看试题解析
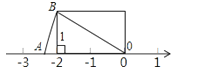20. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2011次运动后，动点P的坐标是．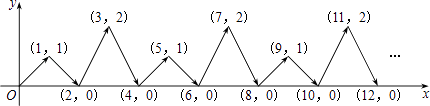

查看试题解析

三、解答题

21. 计算：

(1)、 $(\sqrt{8} - \sqrt{\frac{1}{2}}) \times 3 \sqrt{2}$

(2)、 $\frac{\sqrt{32} + \sqrt{8}}{\sqrt{2}} - \sqrt{\frac{1}{6}} \times \sqrt{18}$

查看试题解析
22. 已知 $\sqrt{7}$ 的整数部分是 a，小数部分是 b ，求 b（ $\sqrt{7}$ + a）的值

查看试题解析
23. 已知直线y=kx+b与x轴交于点A（8，0），与y 轴交于点B（0，6）

(1)、求AB的长；

(2)、求k、b的值。

查看试题解析
24. 已知：y-2与x成正比例，且x=2时，y=4.

(1)、求y与x之间的函数关系式；

(2)、若点M（m，3）在这个函数的图象上，求点M的坐标。

查看试题解析
25. △ABC在直角坐标系内的位置如图所示．

(1)、在这个坐标系内画出△A₁B₁C₁ ，使△A₁B₁C₁与△ABC关于y轴对称；

(2)、求△ABC的面积．

查看试题解析
26. 如图，一架长25米的梯子，斜靠在竖直的墙上，这时梯子底端离墙7米．

(1)、此时梯子顶端离地面多少米？

(2)、若梯子顶端下滑4米，那么梯子底端将向左滑动多少米？

查看试题解析
27. 我们已经知道 $(\sqrt{13} + 3) (\sqrt{13} - 3) = 4$ ，因此将 $\frac{8}{\sqrt{13} - 3}$ 分子、分母同时乘“ $\sqrt{13} + 3$ ”，分母就变成了4.请仿照这种方法化简

(1)、 $\frac{1}{2 + \sqrt{3}}$

(2)、 $\frac{1}{1 + \sqrt{2}} + \frac{1}{\sqrt{2} + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{4}} + \frac{1}{\sqrt{4} + \sqrt{5}}$

查看试题解析
28. 分析探索题：细心观察如图，认真分析各式，然后解答问题。
OA₂²=( $\sqrt{1}$ )²＋1＝2       $S_{1} = \frac{\sqrt{1}}{2}$ ；
OA₃²=( $\sqrt{2}$ )²＋1＝3       $S_{2} = \frac{\sqrt{2}}{2}$ ；
OA₄²=( $\sqrt{3}$ )²＋1＝4       $S_{3} = \frac{\sqrt{3}}{2}$ …
填空：

(1)、请写出含有n（n为正整数）的等式S_n=；

(2)、推算出OA₁₀=。

(3)、求S₁²+S₂²+S₃²+…+S₁₀²的值。

查看试题解析