初中数学华师大版八年级上学期第14章测试卷

试卷更新日期：2019-11-12 类型：同步测试

进入出卷网下载

一、单选题

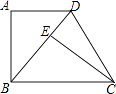
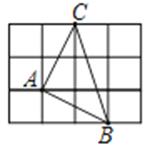
1. 以下列各组数为边长，能构成直角三角形的是（）

A、2，3，4 B、3，4，6 C、5，12，13 D、1，2，3

查看试题解析
2. 如图，将△ABC放在正方形网格图中（图中每个小正方形的边长均为1），点A，B，C恰好在网格图中的格点上，那么△ABC中BC的高是（）

A、 $\frac{\sqrt{10}}{2}$ B、 $\frac{\sqrt{10}}{4}$ C、 $\frac{\sqrt{10}}{5}$ D、 $\sqrt{5}$

查看试题解析
3. 下列语句：①每一个外角都等于 $60^{\circ}$ 的多边形是六边形；②“反证法”就是举反例说明一个命题是假命题；③“等腰三角形两底角相等”的逆命题是真命题；④分式值为零的条件是分子为零且分母不为零，其中正确的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 如图，将 $Rt Δ A B C$ 绕点 $A$ 按顺时针旋转一定角度得到 $Rt Δ A D E$ ，点 $B$ 的对应点 $D$ 恰好落在 $B C$ 边上.若 $A C = 2 \sqrt{3}$ ， $∠ B = 60 °$ ，则 $C D$ 的长为（）

A、1 B、 $\sqrt{3}$ C、2 D、 $4 - \sqrt{3}$

查看试题解析
5. 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方A、B、C、D的边长分别是3、5、2、3，则最大正方形E的面积是（）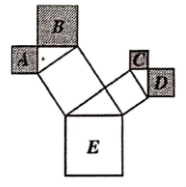

A、13 B、26 C、34 D、47

查看试题解析
6. 如图所示，有一个高18cm，底面周长为24cm的圆柱形玻璃容器，在外侧距下底1cm的点S处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一只苍蝇，则急于捕获苍蝇充饥的蜘蛛所走的最短路径的长度是（）

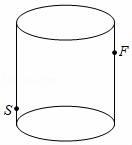A、16cm B、18cm C、20cm D、24cm

查看试题解析

二、填空题

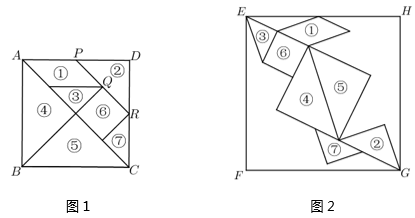
7. 七巧板是我国祖先的一项卓越创造，被誉为“东方魔板”. 由边长为4√2的正方形ABCD可以制作一副如图1所示的七巧板，现将这副七巧板在正方形EFGH内拼成如图2所示的“拼搏兔”造型（其中点Q、R分别与图2中的点E、G重合，点P在边EH上），则“拼搏兔”所在正方形EFGH的边长是.

查看试题解析

三、解答题

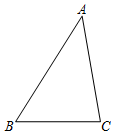
8. 在△ABC中，∠C=30°，AC=4cm，AB=3cm，求BC的长.

查看试题解析
9. 已知：Rt△ABC， $∠$ C=90°，三边长分别为 $a$ , $b$ ， $c$ ，两直角边 $a$ ， $b$ 满足： ${(a^{2} + b^{2})}^{2} - 2 (a^{2} + b^{2}) - 15 = 0$ .求斜边 $c$ .

查看试题解析
10. 如图，△ABC的边AB=8，BC=5，AC=7．求BC边上的高．

查看试题解析
11. 鲁南高铁临沂段修建过程中需要经过一座小山．如图，施工方计划沿 $A C$ 方向开挖隧道，为了加快施工速度，要在小山的另一侧 $D$ ( $A$ 、 $C$ 、 $D$ 共线)处同时施工．测得 $∠ C A B = 30 °$ ， $A B = 4 k m$ ， $∠ A B D = 105 °$ ，求 $B D$ 的长．

查看试题解析

四、综合题

12. 如图，在四边形ABCD中，AD∥BC，∠A=90°，CE⊥BD于E，AB=EC•

(1)、求证：△ABD≌△ECB；

(2)、若∠EDC=65°，求∠ECB的度数；

(3)、若AD=3，AB=4，求DC的长.

查看试题解析

初中数学华师大版八年级上学期 第14章测试卷

一、单选题

二、填空题

三、解答题

四、综合题

初中数学华师大版八年级上学期第14章测试卷