初中数学华师大版八年级上学期 第14章 14.2 勾股定理的应用

试卷更新日期：2019-11-12 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 如图，一棵大树在离地面6米高的B处断裂，树顶A落在离树底部C的8米处，则大树数断裂之前的高度为（      ）

    A、16米 B、15米 C、24米 D、21米

    查看试题解析

  • 2. 如图，一圆柱高 8cm ，底面半径 2cm ，一只蚂蚁从点 A 爬到点 B 处吃食，要爬行的最短路程（ π 取3）是（    ）

    A、10cm B、12cm C、14cm D、无法确定

    查看试题解析

  • 3. 勾股定理是人类最伟大的科学发现之一，在我国古算书 《周髀算经》 中早有记载。如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积，则一定能求出（   ）

     

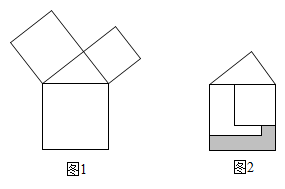    A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和

    查看试题解析

  • 4. 勾股定理是“人类最伟大的十个科学发现之一”，我国对勾股定理得证明是由汉代的赵爽在注解《周髀算经》时给出的，他用来证明勾股定理得图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 5. 《九章算术》是我国古代的数学名著，书中的“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺.问折者高几何？意思是：一根竹子，原高一丈（一丈=10尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部3尺远，问折断处离地面的高度是多少？设折断后离地面的高度为x尺，则可列方程为（   ）
    A、x2–3=（10–x）2 B、x2–32=（10–x）2 C、x2+3=（10–x）2 D、x2+32=（10–x）2

    查看试题解析

  • 6. 在等腰△ABC中，∠ACB=90°，且AC=1.过点C作直线L∥AB，P为直线L上一点，且AP=AB.则点P到BC所在直线的距离是（ ）
    A、1 B、1或 3−12 C、1或 3+12 D、3−12 或 3+12

    查看试题解析

  • 7. 如图图中，不能用来证明勾股定理的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 8. 如图，正方形A，B，C的边长分别为直角三角形的三边长，若正方形A，B的边长分别为3和5，则正方形C的面积为（ ）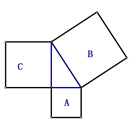

    A、4 B、15 C、16 D、18

    查看试题解析

二、作图题

  • 9. 如图，在7×5的方格纸ABCD中，请按要求画图，且所画格点三角形与格点四边形的顶点均不与点A，B，C，D重合．

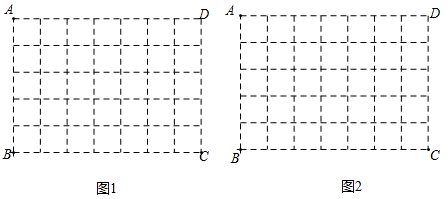    (1)、在图1中画一个格点△EFG，使点E，F，G分别落在边AB，BC，CD上，且∠EFG＝90°；
    (2)、在图2中画一个格点四边形MNPQ，使点M，N，P，Q分别落在边AB，BC，CD，DA上，且MP＝NQ．

    查看试题解析

三、综合题

  • 10. 如图，已知等腰三角形 ABC 的底边 BC 长为10，点 D 是 AC 上的一点，其中 BD=8 ， CD=6 。

    (1)、求证： BD⊥AC ；
    (2)、求 AB 的长。

    查看试题解析

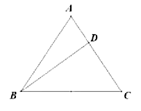  • 11. 如图，铁路MN和铁路PQ在P点处交汇，点A处是某市实验中学，AP=160米，点A到铁路MN的距离为80米，假使火车行驶时，周围100米以内会受到噪音影响.

    (1)、火车在铁路MN上沿PN方向行驶时，学校是否会受到影响?请说明理由；
    (2)、如果受到影响，已知火车的速度是180千米／时，那么学校受到影响的时间是多久?

    查看试题解析

  • 12. 在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中AB＝AC，由于某种原因，由C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H（A、H、B在一条直线上），并新修一条路CH，测得CB＝3千米，CH＝2.4千米，HB＝1.8千米．

    (1)、问CH是否为从村庄C到河边的最近路？（即问：CH与AB是否垂直？）请通过计算加以说明；
    (2)、求原来的路线AC的长．

    查看试题解析