初中数学华师大版八年级上学期 第14章 14.1.3 反证法

试卷更新日期：2019-11-12 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 用反证法证明命题“三角形中至少有一个角大于或等于60°”时，首先应假设这个三角形中（     ）
    A、有一个内角大于60° B、有一个内角小于60° C、每一个内角都大于60° D、每一个内角都小于60°

    查看试题解析

  • 2. 用反证法证明命题“三角形中必有一个内角小于或等于60度”时，应假设（   ）
    A、每一个内角都大于60度 B、每一个内角都小于60度 C、有一个内角大于60度 D、有一个内角小于60度

    查看试题解析

二、填空题

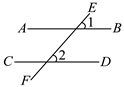
  • 3. 命题“一个三角形中至少有两个锐角”是真命题用反证法证明该命题时,第一步应先假设.

    查看试题解析

  • 4. 如图，直线AB、CD被直线EF所截，∠1、∠2是同位角，如果∠1≠∠2，那么AB与CD不平行．用反证法证明这个命题时，应先假设：.

    查看试题解析

  • 5. 用反证法证明命题：“一个三角形中不能有两个直角”的过程归纳为以下三个步骤：

    ①∠A＋∠B＋∠C＝90°＋90°＋∠C>180°，这与三角形内角和为180°相矛盾，则∠A＝∠B＝90°不成立；②所以一个三角形中不能有两个直角；③假设∠A，∠B，∠C中有两个角是直角，不妨设∠A＝∠B＝90°.正确顺序的序号排列为

    查看试题解析

  • 6. 反证法：先假设命题的不成立，然后推导出与定义、基本事实、已有定理或已知条件相的结果，从而证明命题的结论成立，这种证明方法称为反证法.

    查看试题解析

  • 7. 用反证法证明“三角形三个内角中，至少有一个内角小于或等于60°”．

    已知：∠A，∠B，∠C是△ABC的内角．求证：∠A，∠B，∠C中至少有一个内角小于或等于60°．

    证明：假设求证的结论不成立，那么 ，

    ∴∠A+∠B+∠C＞　 ，

    这与三角形相矛盾．

    ∴假设不成立

    ∴ ．

    查看试题解析

三、解答题

  • 8. 如图，直线AB和直线CD，直线BE和直线CF都被直线BC所截．在下面三个条件中，请你选择其中两个作为题设，剩下的一个作为结论，组成一个真命题并证明．

    ①AB⊥BC，CD⊥BC，②BE∥CF，③∠1＝∠2.

    查看试题解析

  • 9. 如图，等腰直角三角板如图放置．直角顶点C在直线m上，分别过点A、B作AE⊥直线m于点E，BD⊥直线m于点D．

    ①求证： EC=BD ；

    ②若设△AEC三边分别为a、b、c，利用此图证明勾股定理．

    查看试题解析

四、综合题

  • 10. 如图，已知等腰三角形 ABC 的底边 BC 长为10，点 D 是 AC 上的一点，其中 BD=8 ， CD=6 。

    (1)、求证： BD⊥AC ；
    (2)、求 AB 的长。

    查看试题解析