初中数学华师大版八年级上学期 第14章 14.1.1 直角三角形三边的关系

试卷更新日期：2019-11-11 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 如图所示，在Rt△ABC中，∠C=90°，AC=11cm，点P从点A出发沿AC以1cm/s的速度移动，点Q从点C出发沿CB以2cm/s的速度移动，如果P，Q分别从A，C两点同时出发，当它们相距10cm时所需的时间为（   ）

    A、3s B、4s C、5s D、3s或1.4s

    查看试题解析

  • 2. 下列三条线段能构成直角三角形的是（   ）
    A、6, 7, 8 B、2, 3, 4 C、3, 4, 6 D、6，8, 10

    查看试题解析

  • 3. 在直线l上有三个正方形m、q、n，若m、q的面积分别为5和11，则n的面积（   ）

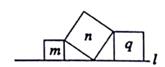    A、4 B、6 C、16 D、55

    查看试题解析

  • 4. 将一根长24cm的筷子置于底面直径为5cm，高为12cm的圆柱水杯中，设筷子露在杯子外面的长度为h，则h的取值范围是（   ）

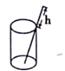    A、12cm≤h≤19cm B、12cm≤h≤13cm C、11cm≤h≤12cm D、5cm≤h≤12cm

    查看试题解析

二、填空题

  • 5. 若直角三角形两条直角边长分别为 5 和 12 ，则斜边上的中线长为 ．

    查看试题解析

  • 6. 若一直角三角形的两直角边长为 3 ，1，则斜边长为 ．

    查看试题解析

三、解答题

  • 7. 如图，一架10米长的梯子斜靠在墙上，刚好梯顶抵达8米高的路灯．当电工师傅沿梯上去修路灯时，梯子下滑到了B′处，下滑后，两次梯脚间的距离为2米，则求此时梯顶离路灯的距离。

    查看试题解析

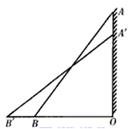  • 8. 如图，△ABC中，AB＝AC ， BC＝4cm ， 作AD⊥BC ， 垂足为D ， 若AD＝4cm ， 求AB的长．

    查看试题解析

  • 9. 如图，在Rt△ABC中，∠C＝90°，AC＝5，AB＝13，求BC．

    查看试题解析

四、综合题

  • 10. 我们学习了勾股定理后，都知道“勾三、股四、弦五”．

    观察：3、4、5；5、12、13；7、24、25；9、40、41；…，发现这些勾股数的勾都是奇数，且从3起就没有间断过．

    (1)、请你根据上述的规律写出下一组勾股数：
    (2)、若第一个数用字母n（n为奇数，且n≥3）表示，那么后两个数用含n的代数式分别表示为和 ， 请用所学知识说明它们是一组勾股数．

    查看试题解析

  • 11. 如图，在△ABC中，AD⊥BC，AD＝12，BD＝16，CD＝5．

    求：

    (1)、△ABC的周长；
    (2)、判断△ABC是否是直角三角形？为什么？

    查看试题解析