河北省邢台市2019届高三上学期理数一轮摸底考试(12月)试卷
试卷更新日期:2019-11-11 类型:月考试卷
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 设 的实部与虚部相等,其中 为实数,则 ( )A、-1 B、-2 C、1 D、23. 某几何体的三视图如图所示,则该几何体的直观图为( )
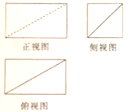 A、
A、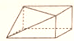 B、
B、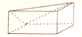 C、
C、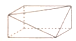 D、
D、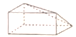 4. 若双曲线 的离心率为2,则其实轴长为( )A、 B、 C、 D、5. 若 ,则 ( )A、 B、 C、 D、6. 函数 的图像大致为( )A、
4. 若双曲线 的离心率为2,则其实轴长为( )A、 B、 C、 D、5. 若 ,则 ( )A、 B、 C、 D、6. 函数 的图像大致为( )A、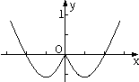 B、
B、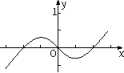 C、
C、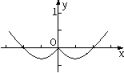 D、
D、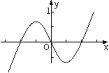 7. 的展开式中有理项共有( )A、4项 B、3项 C、2项 D、1项8. 若 , 满足约束条件 ,则 的最大值为( )A、15 B、30 C、 D、349. 的内角 , , 的对边分别为 , , .已知 , , 成等比数列, ,且 ,则 ( )A、 B、 C、 D、10. 已知点 是抛物线 上的动点,则 的最小值为( )A、3 B、4 C、5 D、611. 将函数 的图像向左平移 个单位长度后,得到 的图像,若函数 在 上单调递减,则正数 的最大值为( )A、 B、1 C、 D、12. 已知函数 ,若函数 恰有5个零点,且最小的零点小于-4,则 的取值范围是( )A、 B、 C、 D、
7. 的展开式中有理项共有( )A、4项 B、3项 C、2项 D、1项8. 若 , 满足约束条件 ,则 的最大值为( )A、15 B、30 C、 D、349. 的内角 , , 的对边分别为 , , .已知 , , 成等比数列, ,且 ,则 ( )A、 B、 C、 D、10. 已知点 是抛物线 上的动点,则 的最小值为( )A、3 B、4 C、5 D、611. 将函数 的图像向左平移 个单位长度后,得到 的图像,若函数 在 上单调递减,则正数 的最大值为( )A、 B、1 C、 D、12. 已知函数 ,若函数 恰有5个零点,且最小的零点小于-4,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 已知向量 , 满足 , , ,则 .14. 小周公司的班车早上7点到达 地,停留15分钟.小周在6:50至7:45之间到达 地搭乘班车,且到达 地的时刻是随机的,则他能赶上公司班车的概率为 .15. 已知 , ,则 的近似数为 . (结果精确到0.001)16. 已知正四棱锥 的底面边长和高均为3, , 分别是棱 , 上一点,且满足 , ,过 做平面与线段 , 分别交于 , ,则四棱锥 的体积的最小值为 .
三、解答题
-
17. 已知数列 是等差数列,且 , .(1)、求 的通项公式;(2)、设 ,求数列 的前 项和 .18. 如图,在三棱锥 中, 平面 ,且 ,
 (1)、证明:三棱锥 为鳖臑;(2)、若 为棱 的中点,求二面角 的余弦值.注:在《九章算术》中鳖臑是指四面皆为直角三角形的三棱锥.19. 2018年中秋季到来之际,某超市为了解中秋节期间月饼的销售量,对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量(单位: )进行了问卷调查,得到如下频率分布直方图:
(1)、证明:三棱锥 为鳖臑;(2)、若 为棱 的中点,求二面角 的余弦值.注:在《九章算术》中鳖臑是指四面皆为直角三角形的三棱锥.19. 2018年中秋季到来之际,某超市为了解中秋节期间月饼的销售量,对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量(单位: )进行了问卷调查,得到如下频率分布直方图: (1)、求频率分布直方图中 的值;(2)、已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的 ,请根据人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求?(3)、由频率分布直方图可以认为,该销售范围内消费者的月饼购买量 服从正态分布 ,其中样本平均数 作为 的估计值,样本标准差 作为 的估计值,设 表示从该销售范围内的消费者中随机抽取10名,其月饼购买量位于 的人数,求 的数学期望.
(1)、求频率分布直方图中 的值;(2)、已知该超市所在销售范围内有20万人,并且该超市每年的销售份额约占该市场总量的 ,请根据人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求?(3)、由频率分布直方图可以认为,该销售范围内消费者的月饼购买量 服从正态分布 ,其中样本平均数 作为 的估计值,样本标准差 作为 的估计值,设 表示从该销售范围内的消费者中随机抽取10名,其月饼购买量位于 的人数,求 的数学期望.附:经计算得 ,若随机变量 服从正态分布 ,则 , .
20. 在直角坐标系 中,椭圆 的中心在原点,焦点在 轴上,且过点 ,若 的两焦点与其中一个顶点能构成一个等边三角形. (1)、求 的方程.(2)、已知过 的两条直线 , (斜率都存在)与 的右半部分( 轴右侧)分别相交于 , 两点,且 的面积为 ,试判断 , 的斜率之积是否为定值?若是,求出定值;若不是,说明理由.
(1)、求 的方程.(2)、已知过 的两条直线 , (斜率都存在)与 的右半部分( 轴右侧)分别相交于 , 两点,且 的面积为 ,试判断 , 的斜率之积是否为定值?若是,求出定值;若不是,说明理由.