吉林省长春市朝阳区2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2019-11-08 类型：期中考试
一、选择题(每小题3分，共24分)
-
1. 9的平方根是（ ）A、-3 B、3 C、±3 D、±2. 和数轴上的点一对应的是（ ）A、整数 B、有理数 C、无理数 D、实数3. 下列运算中，正确的是（ ）A、 B、 C、 D、4. 下列命题是假命题的是（ ）A、两边及其夹角分别相等的两个三角形全等 B、两角及其夹边分别相等的两个三角形全等 C、两边分别相等且其中一组等边的对相等的两个二角形全等 D、两角分别相等凡其中·组等角的对边相等的两个三角形全等5. 如果(a+b)2=11，(a-b)2=7，则ab的值是（ ）A、2 B、1 C、-2 D、-16. 如图，若将图①中的阴影部分剪下来，拼成如图②所示的长方形，比较两图阴影部分的面积，可以得到乘法公式（ ）
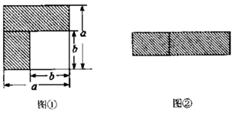A、(a-b)2=a2-2ab+b2 B、a(a-b)=a2-ab C、a2-b2=(a-b)2 D、a2-b2=(a+b)(a-b)7. 如图，在数轴上标注了四段范围，则表示 的点落在第 段。（ ）
A、① B、② C、③ D、④8. 若(x2+px+8)(x2-3x+q)的展开式中，不含x3和x2项，则p，q的值为（ ）A、p=3，q=1 B、p=0，q=0 C、p=-3，q=-9 D、p=-3，q=1二、填空题(每小题3分，共18分)
-
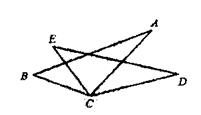
9. -0.008的立方根是 。10. 多项式6ab2x-3a2by+12a2b2的公因式是。11. 以a=为反例，可以判断命题“对任意实数a，它的平方是正数”是假命题。12. 订算：-4a3b2c·3ab3=。13. 如图，∠ACD=∠BCE，EC=BC，要使△ABC≌△DEC，则可以添加的一个条件是 。
14. 数学活动课上，小敏、小颖分别画了△ABC和△DEF，如图所示，如果把小敏画的三角形的面积记作S△ABC ， 小颖画的三角形的面积记作S△DEF ， 那么S△ABCS△DEF。(填“>””<”或”=”)
三、解答题(本大题共9小题，共78分)
-
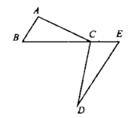
15. 计算：(1)、(2)、3a(a-b+2)(3)、(-3x+2)(-3x+6)(4)、(6x3-15x2+3x) ÷3x16. 把下列多项式分解因式：(1)、a2x2-a2y2(2)、4x2-8xy+4y217. 利用乘法公式计算；(1)、20192-2018×2020(2)、99.8218. 如图，C为BE上一点，AB∥DE，AB=CE，∠BAC=∠ECD．求证：AC=CD。
19. 先化简，再求值：(a+b)(a-b)+a(2b-a)，其中a= ，b=-2。20. 有一个长方体游泳池，它的长为4a2b，宽为ab2 ， 高为ab若要在该游泳池的四周及底面贴上边长为b的正方形防渗漏瓷砖，共需用这样的瓷砖多少块?(用含a、b的代数式表示)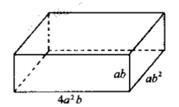
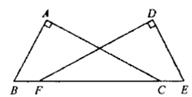
21. 如图，B、F、C、E在同一条直线上，∠A=∠D=90°，AB=DE，BF=CE。求证：∠B=∠E。
22. 如图，在△ABC中，BE、CF分别是边AC、AB上的高，相交于点O，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连结AD、AG。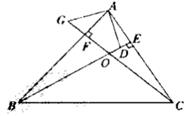
(1)、求证：AD=AG．(2)、写出AD与AG的位置关系，请说明理由。23. 如图，在△ABC中，∠ACB=90，AC=6，BC=8．点P从点A出发，沿折线AC-CB以每秒1个单位长度的速度向终点B运动，点Q从点B出发沿折线BC-CA以每秒3个单位长度的速度向终点A运动，P、Q两点同时出发．分别过P、Q两点作PE⊥l于E，QF⊥l于F．设点P的运动时间为t(秒)
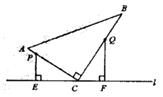(1)、当P、Q两点相遇时，求t的值。(2)、在整个运动过程中，求CP的长(用含t的代数式表示)。(3)、当△PEC与△QFC全等时，直接写出所有满足条件的CQ的长。