初中数学北师大版九年级上学期第六章测试卷

试卷更新日期：2019-11-06 类型：单元试卷

进入出卷网下载

一、单选题

1. 已知点(2，-1)在反比例函数y= $\frac{k}{x}$ (k≠0)的图象上，则这个函数图象一定经过点（）

A、(-2，-1) B、( $- \sqrt{2}$ ， $\sqrt{2}$ ) C、(6， $- \frac{1}{2}$ ) D、( $- \sqrt{3}$ ，1)

查看试题解析
2. 已知点(x₁ ， y₁)和点(x₂ ， y₂)在反比例函数y= $\frac{k}{x}$ (k<0)的图象上，若x₁<x₂ ，则（）

A、(x₁+x₂)(y₁+y₂)<0 B、(x₁+x₂)(y₁+y₂)>0 C、x₁x₂(x₁-x₂)(y₁-y₂)<0 D、x₁x₂(x₁-x₂)(y₁-y₂)>0

查看试题解析
3. 已知点A（-1，m）,B（1，m），C（2，m-n）（n＞0）在同一个函数的图象上，这个函数可能是（）

A、y=x B、 $y = - \frac{2}{x}$ C、 $y = x^{2}$ D、 $y = - x^{2}$

查看试题解析
4. 如图，点A是反比例函数y= $\frac{k}{x}$ 在第一象限图象上一点，连接OA，过点A作AB∥x轴(点B在点A右侧)，连接OB，若∠1=∠2，且点B的坐标是(8，4)，则k的值是（）

A、6 B、8 C、12 D、16

查看试题解析
5. 已知A(1,y₁),B(2,y₂),C(－3,y₃)都在反比例函数 $y = \frac{k}{x}$ (k＞0)的图象上,则y₁,y₂,y₃的大小关系是（）

A、y₂＞y₁＞y₃ B、y₁＞y₂＞y₃ C、y₃＞y₂＞y₁ D、y₁＞y₃＞y₂

查看试题解析

二、填空题

6. 如图，已知反比例函数y= $\frac{k}{x}$ (x>0)的图象经过点A(4，5)，若在该图象上有一点P，使得∠AOP=45°，则点P的坐标是。

查看试题解析
7. 已知，反比例函数y= $\frac{k}{x}$ 的图象在第二、四象限内，则k的值可以是。（写出一个满足条件的k的值即可)

查看试题解析

三、综合题

8. 如图，一次函数 $y = m x + n (m \neq 0)$ 的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象交于第二、四象限内的点 $A (a ， 4)$ 和点 $B (8 ， b)$ ．过点 $A$ 作 $x$ 轴的垂线，垂足为点 $C$ ， $Δ A O C$ 的面积为4．

(1)、分别求出 $a$ 和 $b$ 的值；

(2)、结合图象直接写出 $m x + n < \frac{k}{x}$ 的解集；

(3)、在 $x$ 轴上取点 $P$ ，使 $P A - P B$ 取得最大值时，求出点 $P$ 的坐标．

查看试题解析
9. 如图，一次函数 $y = - x + 4$ 的图象与反比例 $y = \frac{k}{x}$ （ $k$ 为常数，且 $k$ $\neq 0$ ）的图象交于 $A (1 ， a) ， B$ 两点．

(1)、求反比例函数的表达式及点 $B$ 的坐标；

(2)、在x轴上找一点 $P$ ，使 $P A + P B$ 的值最小，求满足条件的点 $P$ 的坐标及 $Δ P A B$ 的面积．

查看试题解析
10. 如图，矩形ABCD的边BC在x轴上，点A(a，4)和D分别在反比函数y= $\frac{12}{x}$ 和y= $\frac{m}{x}$ (m>0)的图象上．

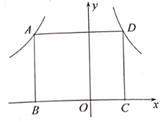(1)、当AB=BC时，求m的值。

(2)、连结OA，OD．当OD平分∠AOC时，求△AOD的周长．

查看试题解析
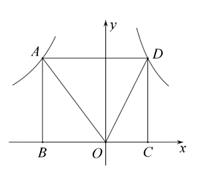11. 如图，一次函数y₁=ax+b的图象和反比例函数y₂= $\frac{k}{x}$ 的附象相交于A(-2，3)和B(m，-1)两点。

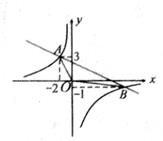(1)、试确定一次函数与反比例函数表达式；

(2)、求△OAB的面积；

(3)、结合图象，直接写出使y₁>y₂成立的x的取值范围。

查看试题解析
12. 为预防传染病，某校定期对教室进行“药熏消毒”．已知药物燃烧阶段，室内每立方米空气中的含药量y(mg)与药物在空气中的持续时间x(min)成正比例；燃烧后，y与x成反比例(如图所示)．现测得药物10分钟燃完，此时教室内每立方米空气含药量为8mg．根据以上信息解答下列问题：

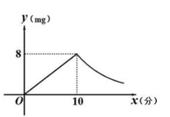(1)、分别求出药物燃烧时及燃烧后y关于x的函数表达式．

(2)、当每立方米空气中的含药量低于1.6mg时，对人体方能无毒害作用，那么从消毒开始，在哪个时段消毒人员不能停留在教室里?

(3)、当室内空气中的含药量每立方米不低于3.2mg的持续时间超过20分钟，才能有效杀灭某种传染病毒．试判断此次消毒是否有效，并说明理由．

查看试题解析

初中数学北师大版九年级上学期 第六章测试卷

一、单选题

二、填空题

三、综合题

初中数学北师大版九年级上学期第六章测试卷