2017年山东省济南市长清区中考数学二模试卷
试卷更新日期:2017-07-14 类型:中考模拟
一、选择题
-
1. 9的算术平方根为( )A、3 B、±3 C、﹣3 D、812.
“天宫二号”是中国载人航天工程中第一个真正意义上的空间实验室,2016年9月15日,“天宫二号”发射取得圆满成功,它的运行轨道距离地球393000米,数据393000米用科学记数法表示为( )
 A、0.393×107米 B、3.93×106米 C、3.93×105米 D、39.3×104米3.
A、0.393×107米 B、3.93×106米 C、3.93×105米 D、39.3×104米3.如图,AB∥CD,直线l交AB于点E,交CD于点F,若∠2=75°,则∠1等于( )
 A、105° B、115° C、125° D、75°4. 如图所示几何体的左视图为( )
A、105° B、115° C、125° D、75°4. 如图所示几何体的左视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 下列计算正确的是( )A、x6+x6=x12 B、(x2)3=x5 C、x﹣1=x D、x2•x3=x56. 东营市某学校组织知识竞赛,共设有20道试题,其中有关中国优秀传统文化试题10道,实践应用试题6道,创新能力试题4道.小婕从中任选一道试题作答,他选中创新能力试题的概率是( )A、 B、 C、 D、7. 分式方程 的解是( )A、x=﹣2 B、x=1 C、x=2 D、x=38. 如图,△ABC经过怎样的平移得到△DEF( )
5. 下列计算正确的是( )A、x6+x6=x12 B、(x2)3=x5 C、x﹣1=x D、x2•x3=x56. 东营市某学校组织知识竞赛,共设有20道试题,其中有关中国优秀传统文化试题10道,实践应用试题6道,创新能力试题4道.小婕从中任选一道试题作答,他选中创新能力试题的概率是( )A、 B、 C、 D、7. 分式方程 的解是( )A、x=﹣2 B、x=1 C、x=2 D、x=38. 如图,△ABC经过怎样的平移得到△DEF( ) A、把△ABC向左平移4个单位,再向下平移2个单位 B、把△ABC向右平移4个单位,再向下平移2个单位 C、把△ABC向右平移4个单位,再向上平移2个单位 D、把△ABC向左平移4个单位,再向上平移2个单位9. 观察下列银行标志,从图案看既是轴对称图形又是中心对称图形的有( )个.
A、把△ABC向左平移4个单位,再向下平移2个单位 B、把△ABC向右平移4个单位,再向下平移2个单位 C、把△ABC向右平移4个单位,再向上平移2个单位 D、把△ABC向左平移4个单位,再向上平移2个单位9. 观察下列银行标志,从图案看既是轴对称图形又是中心对称图形的有( )个. A、1个 B、2个 C、3个 D、4个10. 若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )A、
A、1个 B、2个 C、3个 D、4个10. 若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )A、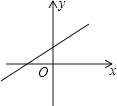 B、
B、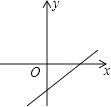 C、
C、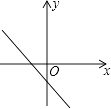 D、
D、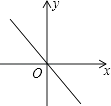 11. 如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC=( )
11. 如图,AB是⊙O的直径,AB=15,AC=9,则tan∠ADC=( )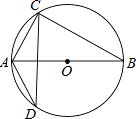 A、 B、 C、 D、12. 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( )
A、 B、 C、 D、12. 如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为( ) A、2 B、 C、1 D、13. 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1 , 使∠D1AC=60°;连接AC1 , 再以AC1为边作第三个菱形AC1C2D2 , 使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )
A、2 B、 C、1 D、13. 如图,在边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1 , 使∠D1AC=60°;连接AC1 , 再以AC1为边作第三个菱形AC1C2D2 , 使∠D2AC1=60°;…,按此规律所作的第2017个菱形的边长为( )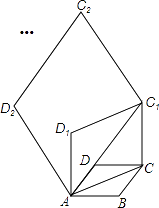 A、( )2016 B、( )2016 C、22017 D、( )201714. 如图1,在四边形ABCD中,AD∥BC,∠B=∠C=60°,P、Q同时从B出发,以每秒1单位长度分别沿B﹣A﹣D﹣C和B﹣C﹣D方向运动至相遇时停止,设运动时间为t(秒),△BPQ的面积为S(平方单位),S与t的函数图象如图2所示,则下列结论错误的个数( )
A、( )2016 B、( )2016 C、22017 D、( )201714. 如图1,在四边形ABCD中,AD∥BC,∠B=∠C=60°,P、Q同时从B出发,以每秒1单位长度分别沿B﹣A﹣D﹣C和B﹣C﹣D方向运动至相遇时停止,设运动时间为t(秒),△BPQ的面积为S(平方单位),S与t的函数图象如图2所示,则下列结论错误的个数( )①当t=4秒时,S=4 ②AD=4
③当4≤t≤8时,S=2 t ④当t=9秒时,BP平分四边形ABCD的面积.
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
15. 计算: +(﹣2)0= .16. 因式分解:a2﹣6a+9= .17. 某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是岁.18.
如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60米2 , 两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为米.
 19. 如图,已知点A在反比例函数y= (x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E.若△BCE的面积为8,则k= .
19. 如图,已知点A在反比例函数y= (x<0)上,作Rt△ABC,点D为斜边AC的中点,连DB并延长交y轴于点E.若△BCE的面积为8,则k= .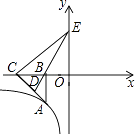 20. 如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
20. 如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 . (填写所有正确结论的序号)

三、解答题
-
21. 根据要求进行计算:(1)、化简:(x﹣2)2+x(x+4)(2)、解不等式组 .22. 根据问题进行证明:(1)、已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P,求证:AP=BQ.
 (2)、如图,已知AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D且∠A=∠D.求∠D的度数.23. 春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.求甲、乙两种商品每件的进价分别是多少元?24. 为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:
(2)、如图,已知AB是⊙O的直径,AC是⊙O的弦,过点C的切线交AB的延长线于点D且∠A=∠D.求∠D的度数.23. 春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.求甲、乙两种商品每件的进价分别是多少元?24. 为了弘扬优秀传统文化,某中学举办了文化知识大赛,其规则是:每位参赛选手回答100道选择题,答对一题得1分,不答或错答不扣分,赛后对全体参赛选手的答题情况进行了相关统计,整理并绘制成如下图表:组别
分数段
频数(人)
频率
1
50≤x<60
30
0.1
2
60≤x<70
45
0.15
3
70≤x<80
60
n
4
80≤x<90
m
0.4
5
90≤x<100
45
0.15

请根据以图表信息,解答下列问题:
(1)、表中m= , n=;(2)、补全频数分布直方图;(3)、在得分前5名的同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学参加区级的比赛,用树状图或列表法求选出的两名同学恰好是一男一女的概率.25. 如图,直线y= x﹣ 与x,y轴分别交于点A,B,与反比例函数y= (k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E. (1)、求点A的坐标.(2)、若AE=AC.
(1)、求点A的坐标.(2)、若AE=AC.①求k的值.
②试判断点E与点D是否关于原点O成中心对称?并说明理由.
26. 如图1,在平面直角坐标系中,O是坐标原点,▱ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2 ),点B在x轴的正半轴上,点E为线段AD的中点,过点E的直线l与x轴交于点F,与射线DC交于点G. (1)、求∠DCB的度数;(2)、当点F的坐标为(﹣4,0)时,求点G的坐标;
(1)、求∠DCB的度数;(2)、当点F的坐标为(﹣4,0)时,求点G的坐标;
(3)、连接OE,以OE所在直线为对称轴,△OEF经轴对称变换后得到△OEF',记直线EF'与射线DC的交点为H.如图2,当点G在点H的左侧时,求证:△DEG∽△DHE.
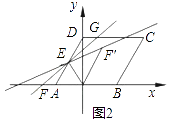 27. 如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
27. 如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边). (1)、求抛物线的解析式及A、B两点的坐标;(2)、在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(1)、求抛物线的解析式及A、B两点的坐标;(2)、在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由; (3)、以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
(3)、以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.