2017年山东省东营市中考数学模拟试卷
试卷更新日期:2017-07-14 类型:中考模拟
一、选择题
-
1. ﹣4的倒数的相反数是( )A、﹣4 B、4 C、﹣ D、2. 下列运算正确的是( )A、5a2+3a2=8a4 B、a3•a4=a12 C、(a+2b)2=a2+4b2 D、﹣ =﹣43. 如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( )度.
 A、70 B、65 C、60 D、554. 如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( )
A、70 B、65 C、60 D、554. 如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 下列说法不一定成立的是( )A、若a>b,则a+c>b+c B、若a+c>b+c,则a>b C、若a>b,则a>b D、若a>b , 则a>b6. 今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )A、2种 B、3种 C、4种 D、5种7. 若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )A、
5. 下列说法不一定成立的是( )A、若a>b,则a+c>b+c B、若a+c>b+c,则a>b C、若a>b,则a>b D、若a>b , 则a>b6. 今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )A、2种 B、3种 C、4种 D、5种7. 若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )A、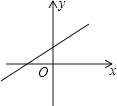 B、
B、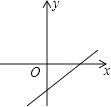 C、
C、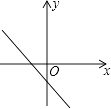 D、
D、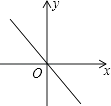 8. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
8. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( ) A、2.5 B、 C、 D、29. 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
A、2.5 B、 C、 D、29. 如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( ) A、 B、 C、 D、10. 边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A、 B、 C、 D、10. 边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 某小区居民王先生改进用水设施,在5年内帮助他居住小区的居民累计节水59800吨,将59800吨用科学记数法表示(结果保留2个有效数字)应为吨.12. 已知关于x的分式方程 ﹣ =1的解为负数,则k的取值范围是 .13. 如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是 .
 14. 如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有个.
14. 如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有个. 15. 有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽取一张,记卡片上的数字为a,则使关于x的不等式组 有解的概率为 .16. 在平行四边形ABCD中,BC边上的高为4,AB=5,AC=2 ,则平行四边形ABCD的周长等于 .17. 如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是 .
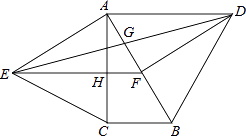
15. 有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽取一张,记卡片上的数字为a,则使关于x的不等式组 有解的概率为 .16. 在平行四边形ABCD中,BC边上的高为4,AB=5,AC=2 ,则平行四边形ABCD的周长等于 .17. 如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是 . 18. 如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
18. 如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH= BD
其中正确结论的为(请将所有正确的序号都填上).
三、解答题
-
19. 根据要求进行计算:(1)、计算:|﹣ |﹣ +2sin60°+( )﹣1+(2﹣ )0(2)、先化简,再求值: ÷(1﹣ ),其中a= ﹣2.20. 为了解某市初三学生的体育测试成绩和课外体育锻炼时间的情况,现从全市初三学生体育测试成绩中随机抽取200名学生的体育测试成绩作为样本.体育成绩分为四个等次:优秀、良好、及格、不及格.
体育锻炼时间
人数
4≤x≤6
2≤x<4
43
0≤x<2
15
 (1)、试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数;(2)、统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表(如图表所示),请将图表填写完整(记学生课外体育锻炼时间为x小时);(3)、全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”,请估计这些学生中课外体育锻炼时间不少于4小时的学生人数.21. 某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
(1)、试求样本扇形图中体育成绩“良好”所对扇形圆心角的度数;(2)、统计样本中体育成绩“优秀”和“良好”学生课外体育锻炼时间表(如图表所示),请将图表填写完整(记学生课外体育锻炼时间为x小时);(3)、全市初三学生中有14400人的体育测试成绩为“优秀”和“良好”,请估计这些学生中课外体育锻炼时间不少于4小时的学生人数.21. 某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系. (1)、请解释图中点D的横坐标、纵坐标的实际意义;(2)、求线段AB所表示的y1与x之间的函数表达式;(3)、当该产品产量为多少时,获得的利润最大?最大利润是多少?22. 如图,正比例函数y=2x的图象与反比例函数y= 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
(1)、请解释图中点D的横坐标、纵坐标的实际意义;(2)、求线段AB所表示的y1与x之间的函数表达式;(3)、当该产品产量为多少时,获得的利润最大?最大利润是多少?22. 如图,正比例函数y=2x的图象与反比例函数y= 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2. (1)、求k的值;(2)、x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.23. 已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.
(1)、求k的值;(2)、x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.23. 已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF. (1)、如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;(2)、如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;(3)、如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.24. 如图1,抛物线y=ax2+bx+4的图象过A(﹣1,0),B(4,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动.
(1)、如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;(2)、如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;(3)、如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.24. 如图1,抛物线y=ax2+bx+4的图象过A(﹣1,0),B(4,0)两点,与y轴交于点C,作直线BC,动点P从点C出发,以每秒 个单位长度的速度沿CB向点B运动,运动时间为t秒,当点P与点B重合时停止运动. (1)、求抛物线的表达式;(2)、如图2,当t=1时,求S△ACP的面积;(3)、如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.
(1)、求抛物线的表达式;(2)、如图2,当t=1时,求S△ACP的面积;(3)、如图3,过点P向x轴作垂线分别交x轴,抛物线于E、F两点.①求PF的长度关于t的函数表达式,并求出PF的长度的最大值;
②连接CF,将△PCF沿CF折叠得到△P′CF,当t为何值时,四边形PFP′C是菱形?