2017年山东省德州市乐陵市中考数学一模试卷

试卷更新日期：2017-07-14 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣2的相反数是（）

A、2 B、﹣2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 下列计算正确的是（）

A、a²•a³=a⁶ B、2a+3a=6a C、a²+a²+a²=3a² D、a²+a²+a²=a⁶

查看试题解析
3. 如图，有一个正方体纸巾盒，它的平面展开图是（）

A、 B、 C、 D、

查看试题解析
4. 若一组数据1、a、2、3、4的平均数与中位数相同，则a不可能是下列选项中的（）

A、0 B、2.5 C、3 D、5

查看试题解析
5. 如图，AB∥CD，AD=CD，∠1=70°，则∠2的度数是（）

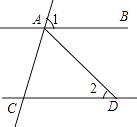A、20° B、35° C、40° D、70°

查看试题解析
6. 在平面直角坐标系中，若点P（m，m﹣n）与点Q（﹣2，3）关于原点对称，则点M（m，n）在（）

A、（2，5） B、（﹣3，2） C、（3，﹣2） D、（3，2）

查看试题解析
7. 如图，已知二次函数y₁= $\frac{2}{3}$ x²﹣ $\frac{4}{3}$ x的图象与正比例函数y₂= $\frac{2}{3}$ x的图象交于点A（3，2），与x轴交于点B（2，0），若0＜y₁＜y₂ ，则x的取值范围是（）

A、0＜x＜2 B、0＜x＜3 C、2＜x＜3 D、x＜0或x＞3

查看试题解析
8. 若在“正三角形、平行四边形、菱形、正五边形、正六边形”这五种图形中随机抽取一种图形，则抽到的图形属于中心对称图形的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
9. 如图，在矩形ABCD中，CD=1，∠DBC=30°．若将BD绕点B旋转后，点D落在DC延长线上的点E处，点D经过的路径 $\hat{D E}$ ，则图中阴影部分的面积是（）

A、 $\frac{π}{3}$ ﹣ $\sqrt{3}$ B、 $\frac{π}{3}$ ﹣ $\frac{\sqrt{3}}{2}$ C、 $\frac{π}{2}$ ﹣ $\sqrt{3}$ D、 $\frac{π}{2}$ ﹣ $\frac{\sqrt{3}}{2}$

查看试题解析
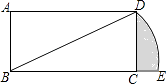10. 若函数 $y = {\begin{matrix} x^{2} + 2 (x \leq 2) \\ 2 x (x > 2) \end{matrix}$ ，则当函数值y=8时，自变量x的值是（）

A、± $\sqrt{6}$ B、4 C、± $\sqrt{6}$ 或4 D、4或﹣ $\sqrt{6}$

查看试题解析
11.
已知点A为某封闭图形边界上一定点，动点P从点A出发，沿其边界顺时针匀速运动一周．设点P运动的时间为x，线段AP的长为y．表示y与x的函数关系的图象大致如图，则该封闭图形可能是（）

A、 B、 C、 D、

查看试题解析
12. 下列命题：
①若a+b+c=0，则b²﹣4ac≥0；

②若b=2a+3c，则一元二次方程ax²+bx+c=0有两个不相等的实数根；

③若b²﹣4ac＞0，则二次函数的图象与坐标轴的公共点的个数是2或3．

其中正确的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题

13. 不等式2x﹣5＞3的解集．

查看试题解析
14. 由中国发起创立的“亚洲基础设施投资银行”的法定资本金为100 000 000 000美元，用科学记数法表示为美元．

查看试题解析
15. 若x²+2（m﹣3）x+16是一个完全平方式，那么m应为．

查看试题解析
16. 若扇形的圆心角为120°的弧长是12πcm，则这个扇形的面积是 cm² ．

查看试题解析
17. 如图，在四边形ABCD中，AD=AB=BC，连接AC，且∠ACD=30°，tan∠BAC= $\frac{2 \sqrt{3}}{3}$ ，CD=3，则AC= ．

查看试题解析

三、解答题

18. 解方程：2sin30°﹣2cos60°+tan45°．

查看试题解析
19. 为鼓励大学生创业，政府制定了小型企业的优惠政策，许多小型企业应运而生．某市统计了该市2015年1﹣5月新注册小型企业的数量，并将结果绘制成如图两种不完整的统计图：

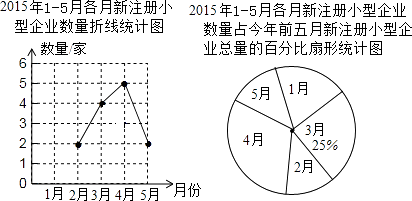(1)、某市2015年1﹣5月份新注册小型企业一共家，请将折线统计图补充完整．

(2)、该市2015年3月新注册小型企业中，只有2家是养殖企业，现从3月新注册的小型企业中随机抽取2家企业了解其经营情况．请以列表或画树状图的方法求出所抽取的2家企业恰好都是养殖企业的概率．

查看试题解析
20. 某玩具厂计划生产一种玩具熊猫，每日最高产量为40只，且每日产出的产品全部售出，已知生产x只熊猫的成本为R（元），售价每只为P（元），且R、P与x的关系式分别为R=500+30x，P=170﹣2x．

(1)、当日产量为多少时每日获得的利润为1750元？

(2)、若可获得的最大利润为1950元，问日产量应为多少？

查看试题解析
21. 如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标（4，2），过点D（0，3）和E（6，0）的直线分别于AB，BC交于点M，N．

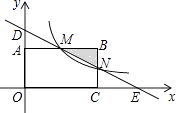(1)、求直线DE的解析式和点M的坐标；

(2)、若反比例函数y= $\frac{m}{x}$ （x＞0）的图象经过点M，求该反比例函数的解析式，并通过计算判断点N是否在该函数的图象上．

查看试题解析
22. 如图，AB、CD为⊙O的直径，弦AE∥CD，连接BE交CD于点F，过点E作直线EP与CD的延长线交于点P，使∠PED=∠C．

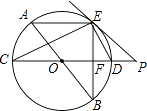(1)、求证：PE是⊙O的切线；

(2)、求证：ED平分∠BEP；

(3)、若⊙O的半径为5，CF=2EF，求PD的长．

查看试题解析
23.
如图，在△ABC中，AB=5，AC=9，S_△_ABC= $\frac{27}{2}$ ，动点P从A点出发，沿射线AB方向以每秒5个单位的速度运动，动点Q从C点出发，以相同的速度在线段AC上由C向A运动，当Q点运动到A点时，P、Q两点同时停止运动，以PQ为边作正方形PQEF（P、Q、E、F按逆时针排序），以CQ为边在AC上方作正方形QCGH．

(1)、求tanA的值；

(2)、设点P运动时间为t，正方形PQEF的面积为S，请探究S是否存在最小值？若存在，求出这个最小值，若不存在，请说明理由；

(3)、当t为何值时，正方形PQEF的某个顶点（Q点除外）落在正方形QCGH的边上，请直接写出t的值．

查看试题解析
24.
如图，二次函数y=x²+px+q（p＜0）的图象与x轴交于A、B两点，与y轴交于点C（0，﹣1），△ABC的面积为 $\frac{5}{4}$ ．

(1)、求该二次函数的关系式；

(2)、过y轴上的一点M（0，m）作y轴的垂线，若该垂线与△ABC的外接圆有公共点，求m的取值范围；

(3)、在该二次函数的图象上是否存在点D，使四边形ACBD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由．

查看试题解析