2017年山东省滨州市无棣县中考数学一模试卷

试卷更新日期：2017-07-14 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣ $\sqrt{2017}$ 的绝对值是（）

A、﹣ $\frac{\sqrt{2017}}{2017}$ B、 $\sqrt{2017}$ C、﹣ $\sqrt{2017}$ D、﹣2017

查看试题解析
2. 若m﹣n=﹣1，则（m﹣n）²﹣2m+2n的值是（）

A、3 B、2 C、1 D、﹣1

查看试题解析
3. 下列调查中，①调查本班同学的视力；②调查一批节能灯管的使用寿命；③为保证“神舟九号”的成功发射，对其零部件进行检查；④对乘坐某班次客车的乘客进行安检．其中适合采用抽样调查的是（）

A、① B、② C、③ D、④

查看试题解析
4. 关于x的一元二次方程 kx²+2x﹣1=0有两个不相等实数根，则k 的取值范围是（）

A、k＞﹣1 B、k≥﹣1 C、k≠0 D、k＞﹣1且k≠0

查看试题解析
5. 如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD=2 $\sqrt{3}$ ，则阴影部分图形的面积为（）

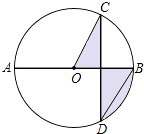A、4π B、2π C、π D、 $\frac{2 π}{3}$

查看试题解析
6. 如图，∠A=70°，O是AB上一点，直线OD与AB所夹的∠BOD=82°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转（）

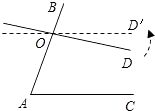A、8° B、10° C、12° D、18°

查看试题解析
7. 如图，平行四边形ABCD中，E为AD的中点，已知△DEF的面积为S，则四边形ABCE的面积为（）

A、8S B、9S C、10S D、11S

查看试题解析
8. 定义：点A（x，y）为平面直角坐标系内的点，若满足x=y，则把点A叫做“平衡点”．例如：M（1，1），N（﹣2，﹣2）都是“平衡点”．当﹣1≤x≤3时，直线y=2x+m上有“平衡点”，则m的取值范围是（）

A、0≤m≤1 B、﹣3≤m≤1 C、﹣3≤m≤3 D、﹣1≤m≤0

查看试题解析
9. 已知四边形ABCD是平行四边形，对角线AC与BD相交于点O，那么下列结论中正确的是（）

A、当AB=BC时，四边形ABCD是矩形 B、当AC⊥BD时，四边形ABCD是矩形 C、当OA=OB时，四边形ABCD是矩形 D、当∠ABD=∠CBD时，四边形ABCD是矩形

查看试题解析
10. 货车行驶25千米与小车行驶35千米所用时间相同，已知小车每小时比货车多行驶20千米，求两车的速度各为多少？设货车的速度为x千米/小时，依题意列方程正确的是（）

A、 $\frac{25}{x} = \frac{35}{x - 20}$ B、 $\frac{25}{x - 20} = \frac{35}{x}$ C、 $\frac{25}{x} = \frac{35}{x + 20}$ D、 $\frac{25}{x + 20} = \frac{35}{x}$

查看试题解析
11. 如图，AB=4，射线BM和AB互相垂直，点D是AB上的一个动点，点E在射线BM上，BE= $\frac{1}{2}$ DB，作EF⊥DE并截取EF=DE，连结AF并延长交射线BM于点C．设BE=x，BC=y，则y关于x的函数解析式是（）

A、y=﹣ $\frac{12 x}{x - 4}$ B、y=﹣ $\frac{2 x}{x - 1}$ C、y=﹣ $\frac{3 x}{x - 1}$ D、y=﹣ $\frac{8 x}{x - 4}$

查看试题解析
12.
在等腰Rt△ABC中，∠C=90°，AC=8，F是AB边上的中点，点D、E分别在AC、BC边上运动，且保持AD=CE．连接DE、DF、EF．在此运动变化的过程中，下列结论：
①△DFE是等腰直角三角形；
②四边形CDFE不可能为正方形；
③四边形CDFE的面积保持不变；
④△CDE面积的最大值为8．
其中正确的结论有（）个．

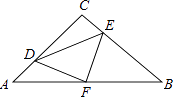A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 计算： $\sqrt[3]{8}$ ﹣ $\sqrt{\frac{1}{3}}$ × $\sqrt{27}$ ×3^﹣¹= ．

查看试题解析
14. 化简： $\frac{x^{2} - 1}{x}$ ÷（1﹣ $\frac{1}{x}$ ）= ．

查看试题解析
15. 如图，Rt△ABC中，∠ABC=90°，AB=BC=2，将△ABC绕点C逆时针旋转60°，得到△MNC，连接BM，那么BM的长是．

查看试题解析
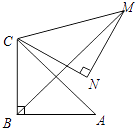16. 已知点A（1，5），B（4，2），点P在x轴上，当AP+BP最小时，点P的坐标为．

查看试题解析
17. 如图，直线l⊥x轴于点P，且与反比例函数y₁= $\frac{k_{1}}{x}$ （x＞0）及y₂= $\frac{k_{2}}{x}$ （x＞0）的图象分别交于点A，B，连接OA，OB，已知△OAB的面积为3，则k₁﹣k₂= ．

查看试题解析
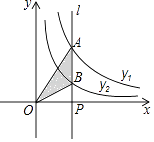18. 观察下列各式：
1³=1² ， 1³+2³=3² ， 1³+2³+3³=6² ， 1³+2³+3³+4³=10² ， …猜想：1³+2³+…+n³（n是正整数）= ．

查看试题解析

三、解答题

19. 解不等式组： ${\begin{matrix} 2 x + 1 \geq - 1 \\ \frac{1 + 2 x}{3} > x - 1 \end{matrix}$ ，并把不等式组的解集在数轴上表示出来．

查看试题解析
20. 如图，等边△ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP=∠ACQ，BP=CQ．判断△APQ的形状，并说明理由．

查看试题解析
21. 为了解外来务工子女就学情况，某校对七年级各班级外来务工子女的人数情况进行了统计，发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况，并制成如下两幅统计图：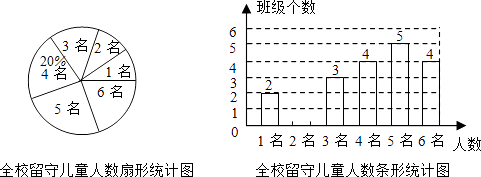

(1)、求该校七年级平均每个班级有多少名外来务工子女？并将该条形统计图补充完整；

(2)、学校决定从只有2名外来务工子女的这些班级中，任选两名进行生活资助，请用列表法或画树状图的方法，求出所选两名外来务工子女来自同一个班级的概率．

查看试题解析
22.
如图，AD是△ABC的角平分线，以AD为弦的⊙O交AB、AC于E、F，已知EF∥BC．

(1)、求证：BC是⊙O的切线；

(2)、若已知AE=12，CF=6，求DE的长．

查看试题解析
23. 小宇想测量位于池塘两端的A、B两点的距离．他沿着与直线AB平行的道路EF行走，当行走到点C处，测得∠ACF=45°，再向前行走100米到点D处，测得∠BDF=60°．若直线AB与EF之间的距离为60米，求A、B两点的距离．

查看试题解析
24. 如图：抛物线y=ax²+bx+c交y轴于点C（0，4），对称轴x=2与x轴交于点D，顶点为M，且DM=OC+OD，

(1)、求抛物线的解析式；

(2)、设点P（x，y）是第一象限内该抛物线上的一个动点，△PCD的面积为S，求S关于x的函数关系式，写出自变量x的取值范围，并求当x取多少时，S的值最大，最大是多少？

查看试题解析