备考2020年高考数学一轮复习：64 二项分布与正态分布（理科专用）

试卷更新日期：2019-11-05 类型：一轮复习

进入出卷网下载

一、单选题

1. 已知随机变量 $ξ$ 服从正态分布 $N (2018, σ^{2}) (σ > 0)$ ，则 $P (ξ < 2018)$ 等于（）

A、 $\frac{1}{1009}$ B、 $\frac{1}{2018}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
2. 在某项测量中测量结果 $X ~ N (3, σ^{2}) (σ > 0)$ ，若X在 $(3, 6)$ 内取值的概率为0.3，则X在 $(0, + \infty)$ 内取值的概率为（）

A、0.2 B、0.4 C、0.8 D、0.9

查看试题解析
3. 已知三个正态分布密度函数 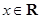$φ_{i} (x) = \frac{1}{\sqrt{2 π σ_{i}}} e^{- \frac{{(x - μ_{i})}^{2}}{2 σ_{i}^{2}}}$ （， $i = 1 ， 2 ， 3$ ）的图象如图所示则（）

A、 $μ_{1} < μ_{2} = μ_{3} ， σ_{1} = σ_{2} > σ_{3}$ B、 $μ_{1} > μ_{2} = μ_{3} ， σ_{1} = σ_{2} < σ_{3}$ C、 $μ_{1} = μ_{2} < μ_{3} ， σ_{1} < σ_{2} = σ_{3}$ D、 $μ_{1} < μ_{2} = μ_{3} ， σ_{1} = σ_{2} < σ_{3}$

查看试题解析
4. 某学校高三模拟考试中数学成绩 $X$ 服从正态分布 $N (75, 121)$ ，考生共有1000人，估计数学成绩在75分到86分之间的人数约为（）人．
参考数据： $P (μ - σ < X < μ + σ) = 0.6826$ ， $P (μ - 2 σ < X < μ + 2 σ) = 0.9544$ ）

A、261 B、341 C、477 D、683

查看试题解析
5. 设随机变量 $ξ \sim B (3 ， p)$ ，若 $P (ξ \geq 1) = \frac{19}{27}$ ，则 $D ξ =$ （）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $1$ D、 $2$

查看试题解析
6. 已知袋中装有除颜色外完全相同的5个球，其中红球2个，白球3个，现从中任取1球，记下颜色后放回，连续摸取3次，设 $ξ$ 为取得红球的次数，则 $P (ξ = 2) =$ （）

A、 $\frac{4}{25}$ B、 $\frac{36}{125}$ C、 $\frac{9}{25}$ D、 $\frac{54}{125}$

查看试题解析
7. 设随机变量 $ξ$ 服从正态分布 $N (1 ， 4)$ ，且 $P (ξ > 2) = 0.3$ ，则 $P (0 < ξ < 1) =$ （）

A、 $0.15$ B、 $0.2$ C、 $0.4$ D、 $0.7$

查看试题解析
8. 某电子管正品率为 $\frac{3}{4}$ ，次品率为 $\frac{1}{4}$ ，现对该批电子管进行测试，那么在五次测试中恰有三次测到正品的概率是（）

A、 $C_{5}^{3} {(\frac{3}{4})}^{3}$ B、 $C_{5}^{2} {(\frac{1}{4})}^{2}$ C、 $C_{5}^{2} {(\frac{3}{4})}^{2} {(\frac{1}{4})}^{3}$ D、 $C_{5}^{3} {(\frac{3}{4})}^{3} {(\frac{1}{4})}^{2}$

查看试题解析
9. 在一次共有10000名考生的某市高二的联考中，这些学生的数学成绩 $ξ$ 服从正态分布 $N (100 ， σ^{2})$ ，且 $P (80 < ξ ⩽ 100) = 0.4$ .若按成绩分层抽样的方式抽取100份试卷进行分析，应从120分以上的试卷中抽取（）

A、20份 B、15份 C、10份 D、5份

查看试题解析
10. 某群体中的每位成员使用移动支付的概率都为 $p$ ，各成员的支付方式相互独立，设 $X$ 为该群体的10位成员中使用移动支付的人数， $D X = 2.4$ ， $P (X = 4) < P (X = 6)$ ，则 $p =$ （）

A、0.7 B、0.6 C、0.4 D、0.3

查看试题解析
11. 某个部件由三个元件按如图所示的方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作.设三个电子元件的使用寿命(单位：时)均服从正态分布N(1000，502)，且各个元件能否正常工作相互独立，那么该部件的使用寿命超过1000小时的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{3}{8}$ C、 $\frac{3}{4}$ D、 $\frac{1}{2}$

查看试题解析
12. 已知参加某次考试的10万名理科考生的数学成绩 $ξ$ 近似地服从正态分布 $N (70, 25)$ ，估算这些考生中数学成绩落在 $(75, 80]$ 内的人数为（）
（附： $Z ~ N (μ, σ^{2})$ ，则 $P (μ - σ < Z \leq μ + σ) = 0.6826, P (μ - 2 σ < Z \leq μ + 2 σ) = 0.9544$ ）

A、4560 B、13590 C、27180 D、311740

查看试题解析

二、填空题

13. 已知随机变量 $X ~ B (6, \frac{1}{4})$ ，则 $E (X)$ 的值为．

查看试题解析
14. 已知某公司生产的一种产品的质量 $X$ (单位：千克)服从正态分布 $N (100 ， 64)$ .现从该产品的生产线上随机抽取 $10000$ 件产品，则其中质量在区间 $(92 ， 100)$ 内的产品估计有件.
附：若 $X \sim N (μ ， σ^{2})$ ，则 $P (μ - σ < X < μ + σ) \approx 0.6826$ ， $P (μ - 2 σ < X < μ + 2 σ) \approx 0.9544$ .

查看试题解析
15. 已知随机变量 $X ~ N (100, σ^{2}), P (80 < X ⩽ 100) = 0.4$ ，则 $P(X>120)=$

查看试题解析
16. 若 $X \sim N (- 1, σ^{2})$ ，且 $P (- 2 \leq X \leq - 1) = 0.3$ ，则 $P (X \geq 0) =$

查看试题解析
17. 一批产品的二等品率为0.02，从这批产品中每次随机取一件，有放回地抽取100次，若 $X$ 表示抽到的二等品件数，则 $D (X) =$ .

查看试题解析
18. 某地区高二女生的体重 $X$ (单位: $k g$ )服从正态分布 $N (50, 25)$ ,若该地区共有高二女生 $2000$ 人,则体重在区间 $(50, 65)$ 内的女生人数约为

查看试题解析

三、解答题

19. 中山某学校的场室统一使用“欧普照明”的一种灯管，已知这种灯管使用寿命 $ξ$ （单位：月）服从正态分布 $N (μ ， σ^{2})$ ，且使用寿命不少于 $12$ 个月的概率为 $0.8$ ，使用寿命不少于 $24$ 个月的概率为 $0.2$ .

(1)、求这种灯管的平均使用寿命 $μ$ ；

(2)、假设一间课室一次性换上 $4$ 支这种新灯管，使用 $12$ 个月时进行一次检查，将已经损坏的灯管换下（中途不更换），求至少两支灯管需要更换的概率.

查看试题解析
20. 已知某种零件的尺寸ξ(单位：mm)服从正态分布，其正态曲线在(0,80)上是增函数，在(80，＋∞)上是减函数，且f(80)＝ $\frac{1}{8 \sqrt{2 π}}$ .

(1)、求概率密度函数；

(2)、估计尺寸在72mm～88mm间的零件大约占总数的百分之几？

查看试题解析
21. 已知随机变量X～N(μ，σ²)，且其正态曲线在(－∞，80)上是增函数，在(80，＋∞)上为减函数，且P(72≤X≤88)＝0.682 6.

(1)、求参数μ，σ的值；

(2)、求P(64<X≤72)．

查看试题解析
22. 某县农民年均收入服从μ＝500元，σ＝20元的正态分布，求：

(1)、此县农民的年均收入在500～520元之间的人数的百分比；

(2)、此县农民的年均收入超过540元的人数的百分比．

查看试题解析