备考2020年高考数学一轮复习：62 几何概型

试卷更新日期：2019-11-05 类型：一轮复习

进入出卷网下载

一、单选题

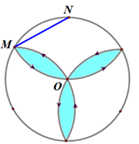
1. 如图，线段MN是半径为2的圆O的一条弦，且MN的长为2.在圆O内，将线段MN绕N点按逆时针方向转动，使点M移动到圆O上的新位置，继续将线段 $M N$ 绕 $M$ 点按逆时针方向转动，使点N移动到圆O上的新位置，依此继续转动……点M的轨迹所围成的区域是图中阴影部分.若在圆 $O$ 内随机取一点，则此点取自阴影部分内的概率为（）．

A、 $4 π - 6 \sqrt{3}$ B、 $1 - \frac{3 \sqrt{3}}{2 π}$ C、 $π - \frac{3 \sqrt{3}}{2}$ D、 $\frac{3 \sqrt{3}}{2 π}$

查看试题解析
2. 下图来自古希腊数学家希波克拉底所研究的几何图形，此图由一个半圆和一个四分之一圆构成，两个阴影部分分别标记为 $A$ 和 $M$ .在此图内任取一点，此点取自 $A$ 区域的概率记为 $P (A)$ ，取自 $M$ 区域的概率记为 $P (M)$ ，则（）

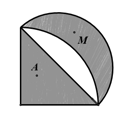A、 $P (A) > P (M)$ B、 $P (A) < P (M)$ C、 $P (A) = P (M)$ D、 $P (A)$ 与 $P (M)$ 的大小关系与半径长度有关

查看试题解析
3. 区间[0，5]上任意取一个实数x，则满足x $\in$ [0，1]的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{4}{5}$ C、 $\frac{5}{6}$ D、 $\frac{1}{4}$

查看试题解析
4. 如图所示，矩形的长和宽分别为5和2，在矩形框内随机撒100粒小麦，恰好有70粒小麦落在阴影部分内，则用随机模拟方法计算得阴影部分的面积为（）

A、3 B、7 C、10 D、5

查看试题解析
5. 如图，直角三角形的两直角边长分别为6和8，三角形内的空白部分是由三个半径为3的扇形构成，向该三角形内随机掷一点，则该点落在阴影部分的概率为（）．

A、 $\frac{3 π}{16}$ B、 $1 - \frac{3 π}{16}$ C、 $\frac{3 π}{8}$ D、 $1 - \frac{3 π}{8}$

查看试题解析
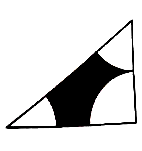6. 在长度为6的线段AB上任取一点C，则AC之间的距离小于2的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{4}$

查看试题解析
7. 已知三棱锥 $S - A B C$ ，在该三棱锥内取一点P，使 $V_{P - A B C} \leq \frac{1}{3} V_{S - A B C}$ 的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{4}{9}$ C、 $\frac{8}{27}$ D、 $\frac{19}{27}$

查看试题解析
8. 在平面直角坐标系 $x O y$ 中，已知点 $A (\sqrt{3} ， 0) ， B (1 ， 2) ， D (3 ， 2)$ ，动点P满足 $\vec{O P} = λ \bar{O A} + μ \vec{O B}$ ，其中 $λ \in [0 ， 1] ， μ \in [0 ， 2] ， λ + μ \in [1 ， 2]$ ，则点P落在三角形 $A B D$ 里面的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{2}{3}$

查看试题解析
9. 圆周率是圆的周长与直径的比值，一般用希腊字母 $π$ 表示．早在公元480年左右，南北朝时期的数学家祖冲之就得出精确到小数点后7位的结果，他是世界上第一个把圆周率的数值计算到小数点后第七位的人，这比欧洲早了约1000年．在生活中，我们也可以通过设计下面的实验来估计 $π$ 的值：从区间 $[- 1 ， 1]$ 内随机抽取200个数，构成100个数对 $(x ， y)$ ，其中满足不等式 $y > \sqrt{1 - x^{2}}$ 的数对 $(x ， y)$ 共有11个，则用随机模拟的方法得到的 $π$ 的近似值为（）

A、 $\frac{78}{25}$ B、 $\frac{72}{25}$ C、 $\frac{25}{7}$ D、 $\frac{22}{7}$

查看试题解析
10. 割补法在我国古代数学著作中称为“出入相补”，刘徽称之为“以盈补虚”，即以多余补不足，是数量的平均思想在几何上的体现.如图揭示了刘徽推导三角形面积公式的方法.在 $Δ A B C$ 内任取一点，则该点落在标记“盈”的区域的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

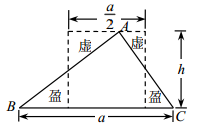查看试题解析
11. “勾股定理”在西方被称为“毕达哥拉斯定理”，三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”用数形结合的方法给出了勾股定理的详细证明．如图所示的“勾股圆方图”中，四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形，若直角三角形中较小的锐角 $α = \frac{π}{6}$ ，现在向该正方形区域内随机地投掷一枚飞镖，飞镖落在小正方形内的概率是（）

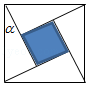A、 $\frac{\sqrt{3}}{4}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{2 - \sqrt{3}}{2}$ D、 $\frac{4 - \sqrt{3}}{4}$

查看试题解析
12. 定义 $min {a ， b} = {\begin{matrix} a ， a \leq b \\ b ， a > b \end{matrix}$ ，由集合 ${(x ， y) | 0 \leq x \leq 2 ， 0 \leq y \leq 1}$ 确定的区域记作 $Ω$ ，由曲线 $C$ ： $y = min {x ， - 2 x + 3}$ 和 $x$ 轴围成的封闭区域记作 $M$ ，向区域 $Ω$ 内投掷12000个点，则落入区域 $M$ 的点的个数为（）

A、4500 B、4000 C、3500 D、3000

查看试题解析
13. 如图所示的图形是弧三角形，又叫莱洛三角形，它是分别以等边三角形 $A B C$ 的三个顶点为圆心，以边长为半径画弧得到的封闭图形.在此图形内随机取一点，则此点取自等边三角形内的概率是（）

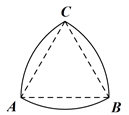A、 $\frac{\sqrt{3}}{2 π - \sqrt{3}}$ B、 $\frac{\sqrt{3}}{2 π - 2 \sqrt{3}}$ C、 $\frac{\sqrt{3}}{π - \sqrt{3}}$ D、 $\frac{\sqrt{3}}{4 π - 2 \sqrt{3}}$

查看试题解析
14. 中国古代数学名著《九章算术》中记载：“圆周与其直径之比被定为3，圆中弓形面积为 $\frac{1}{2} a (a + c)$ （ $c$ 为弦长， $a$ 为半径长与圆心到弦的距离之差）.”据此计算，已知一个圆中弓形所对应的弦长 $c = 6$ ， $a = 1$ ，质点 $M$ 随机投入此圆中，则质点 $M$ 落在该弓形内的概率为（）

A、 $\frac{7}{150}$ B、 $\frac{1}{75}$ C、 $\frac{7}{30}$ D、 $\frac{3}{50}$

查看试题解析
15. 如图， $A B$ 和 $C D$ 是圆 $O$ 两条互相垂直的直径，分别以 $O A$ ， $O B$ ， $O C$ ， $O D$ 为直径作四个圆，在圆 $O$ 内随机取一点，则此点取自阴影部分的概率是（）

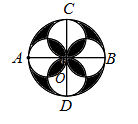A、 $1 - \frac{2}{π}$ B、 $\frac{1}{2} - \frac{1}{π}$ C、 $\frac{2}{π}$ D、 $\frac{1}{π}$

查看试题解析
16. 2018年1月31日晚上月全食的过程分为初亏、食既、食甚、生光、复圆五个阶段，月食的初亏发生在19时48分，20时51分食既，食甚时刻为21时31分，22时08分生光，直至23时12分复圆 $.$ 全食伴随有蓝月亮和红月亮，全食阶段的“红月亮”将在食甚时刻开始，生光时刻结束，一市民准备在19：55至21：56之间的某个时刻欣赏月全食，则他等待“红月亮”的时间不超过30分钟的概率是 $($ $)$

A、 $\frac{5}{11}$ B、 $\frac{7}{12}$ C、 $\frac{4}{11}$ D、 $\frac{11}{12}$

查看试题解析
17. 某公司的班车在7:30，8:00，8:30发车，小明在7:50至8:30之间到达发车站乘坐班车，且到达发车站的时刻是随机的，则他等车时间不超过10分钟的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析

二、填空题

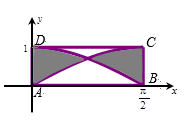
18. 如图，矩形 $A B C D$ 中曲线的方程分别为 $y = \sin x$ ， $y = \cos x$ ，在矩形内随机取一点，则此点取自阴影部分的概率为.

查看试题解析
19. 已知圆 $C ： x^{2} + y^{2} = 4$ 和直线 $l ： y = x$ ，则圆 $C$ 上任意取一点A到直线的距离小于 $\sqrt{3}$ 的概率为．

查看试题解析
20. 设不等式 ${log}_{2} x < 1$ 的解集为 $D$ ，在区间 $[- 3, 5]$ 上随机取一个实数 $x$ ，则 $x \in D$ 的概率为．

查看试题解析
21. 七巧板是我国古代劳动人民的发明之一，被誉为“东方模板”，它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的.如图所示的是一个用七巧板拼成的正方形，若在此正方形中任取一点，则此点取自黑色部分的概率为（）

A、 $\frac{3}{16}$ B、 $\frac{3}{8}$ C、 $\frac{5}{16}$ D、 $\frac{7}{16}$

查看试题解析
22. 如图所示，正方形的四个顶点 $A (- 1 ， - 1)$ ， $B (1 ， - 1)$ ， $C (1 ， 1)$ ， $D (- 1 ， 1)$ ，及抛物线 $y = - {(x + 1)}^{2}$ 和 $y = {(x - 1)}^{2}$ ，若将一个质点随机投入正方形 $A B C D$ 中，则质点落在图中阴影区域的概率是.

查看试题解析