备考2020年高考数学一轮复习：61 古典概型

试卷更新日期：2019-11-05 类型：一轮复习

进入出卷网下载

一、单选题

1. 生物实验室有5只兔子，其中只有3只测量过某项指标。若从这5只兔子中随机取出3只，则恰有2只测量过该指标的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{5}$ C、 $\frac{2}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 《易经》是我国古代预测未来的著作，其中同时抛掷三枚古钱币观察正反面进行预测未知，则抛掷一次时出现两枚正面一枚反面的概率为（）

A、 $\frac{1}{8}$ B、 $\frac{1}{4}$ C、 $\frac{3}{8}$ D、 $\frac{1}{2}$

查看试题解析
3. 2019年，河北等8省公布了高考改革综合方案将采取“3+1+2”模式，即语文、数学、英语必考，然后考生先在物理、历史中选择1门，再在思想政治、地理、化学、生物中选择2门.一名同学随机选择3门功课，则该同学选到物理、地理两门功课的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
4. 打开手机时，忘记了开机的六位密码的第二位和第四位，只记得第二位是7,8,9中的一个数字，第四位是1,2,3中的一个数字，则他输入一次能够开机的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{8}$ C、 $\frac{1}{9}$ D、 $\frac{1}{10}$

查看试题解析
5. 《史记》卷六十五《孙子吴起列传第五》中有这样一道题：齐王与田忌赛马，田忌的上等马优于齐王的中等马，劣于齐王的上等马，田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马，现从双方的马匹中随机选一匹马进行一场比赛、齐王获胜的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{3}{5}$ C、 $\frac{5}{9}$ D、 $\frac{3}{4}$

查看试题解析
6. 某人在微信群中发一个8元“拼手气”红包，被甲、乙、丙三人抢完，若三人均领到整数元，且每人至少领到1元，则甲领到的钱数不少于其他任何人的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{8}{21}$ C、 $\frac{3}{7}$ D、 $\frac{5}{18}$

查看试题解析
7. 若10件产品中包含8件一等品，在其中任取2件，则在已知取出的2件中有1件不是一等品的条件下，另1件是一等品的概率为（）

A、 $\frac{12}{13}$ B、 $\frac{14}{15}$ C、 $\frac{16}{17}$ D、 $\frac{18}{19}$

查看试题解析
8. 从10名高三年级优秀学生中挑选3人担任校长助理，则甲、乙至少有1人入选，而丙没有入选的概率为（）

A、 $\frac{17}{24}$ B、 $\frac{7}{15}$ C、 $\frac{49}{120}$ D、 $\frac{7}{30}$

查看试题解析
9. 从集合 ${a, b, c, d, e}$ 的所有子集中，任取一个，这个集合恰是集合 ${a, b, c}$ 子集的概率是（）

A、 $\frac{3}{5}$ B、 $\frac{2}{5}$ C、 $\frac{1}{4}$ D、 $\frac{1}{8}$

查看试题解析
10. 任取一个三位正整数 $N$ ，则对数 $l o g_{2} N$ 是一个正整数的概率是（）

A、 $\frac{1}{225}$ B、 $\frac{3}{889}$ C、 $\frac{1}{300}$ D、 $\frac{1}{450}$

查看试题解析
11. 大学生小明与另外3名大学生一起分配到某乡镇甲、乙丙3个村小学进行支教，若每个村小学至少分配1名大学生，则小明恰好分配到甲村小学的概率为（）

A、 $\frac{1}{12}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
12. 一个袋子中装有大小形状完全相同的4个白球和3个黑球，从中一次摸出3个球，已知摸出球的颜色不全相同，则摸出白球个数多于黑球个数的概率为（）

A、 $\frac{18}{35}$ B、 $\frac{3}{5}$ C、 $\frac{22}{35}$ D、 $\frac{11}{15}$

查看试题解析

二、填空题

13. 在大小相同的6个球中，2个是红球，4个是白球．若从中任意选取3个，则所选的3个球中至少有1个红球的概率是．（结果用分数表示）

查看试题解析
14. 如图，某建筑工地搭建的脚手架局部类似于一个 $2 \times 2 \times 3$ 的长方体框架，一个建筑工人欲从 A处沿脚手架攀登至B处，则其最近的行走路线中不连续向上攀登的概率为．

查看试题解析
15. 同时转动如图所示的两个转盘，记转盘甲得到的数为x，转盘乙得到的数为y，构成数对（x，y），则所有数对（x，y）中满足xy＝4的概率为.

查看试题解析
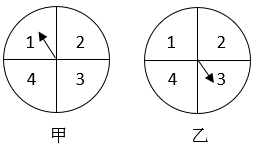16. 从分别写有1,2,3,4的4张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数大于第二张卡片上的数的概率为．

查看试题解析
17. 三位同学参加跳高、跳远、铅球项目的比赛.若每人都选择其中两个项目，则有且仅有两人选择的项目完全相同的概率是.

查看试题解析

三、解答题

18. 甲乙两名篮球运动员分别在各自不同的5场比赛所得篮板球数的茎叶图如图所示，已知两名运动员在各自5场比赛所得平均篮板球数均为10．

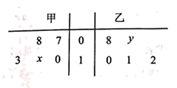(1)、求x，y的值；

(2)、求甲乙所得篮板球数的方差 $S_{甲}^{2}$ 和 $S_{乙}^{2}$ ，并指出哪位运动员篮板球水平更稳定；

(3)、教练员要对甲乙两名运动员篮板球的整体水平进行评估．现在甲乙各自的5场比赛中各选一场进行评估，则两名运动员所得篮板球之和小于18的概率．

查看试题解析
19. 乡大学生携手回乡创业，他们引进某种果树在家乡进行种植试验．他们分别在五种不同的试验田中种植了这种果树100株并记录了五种不同的试验田中果树的死亡数，得到如下数据：

试验田

试验田1

试验田2

试验田3

试验田4

试验田5

死亡数

23

32

24

29

17

（Ⅰ）求这五种不同的试验田中果树的平均死亡数；

（Ⅱ）从五种不同的试验田中随机取两种试验田的果树死亡数，记为x，y，用（x，y）的形式列出所有的基本事件，其中（x，y）和（y，x）视为同一事件，并求 $| x - y | \leq 3 或 | x - y | \geq 9$ 的概率．

查看试题解析
20. 某大学生从全校学生中随机选取 $100$ 名统计他们的鞋码大小，得到如下数据：
鞋码
$35$
$36$
$37$
$38$
$39$
$40$
$41$
$42$
$43$
$44$
合计
男生

$3$
$6$
$8$
$11$
$12$
$6$
$7$
$2$
$55$
女生
$4$
$6$
$12$
$9$
$9$
$2$
$2$

$1$
$45$
以各性别各鞋码出现的频率为概率．

(1)、从该校随机挑选一名学生，求他（她）的鞋码为奇数的概率．

(2)、为了解该校学生考试作弊的情况，从该校随机挑选 $120$ 名学生进行抽样调查．每位学生从装有除颜色外无差别的 $4$ 个红球和 $6$ 个白球的口袋中，随机摸出两个球，若同色，则如实回答其鞋码是否为奇数；若不同色，则如实回答是否曾在考试中作弊．这里的回答，是指在纸上写下“是”或“否”．若调查人员回收到 $32$ 张“是”的小纸条，试估计该校学生在考试中曾有作弊行为的概率．

查看试题解析
21. 口袋中有质地、大小完全相同的5个球，编号分别为1，2，3，4，5．甲先摸出一个球，记下编号为 $a$ ，放回袋中后，乙再摸一个球，记下编号为 $b$ ．

(1)、求“ $a + b = 6$ ”的事件发生的概率；

(2)、若点 $(a, b)$ 落在圆 $x^{2} + y^{2} = 21$ 内，则甲赢，否则算乙赢，这个游戏规则公平吗？试说明理由．

查看试题解析
22. 某高级中学共有学生2000名，各年级男、女生人数如下表：

高一年级

高二年级

高三年级

女生

373

x

y

男生

377

370

z

已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.19.

(1)、求 $x$ 的值；

(2)、现用分层抽样的方法在全校抽取48名学生，问应该在高三年级抽取多少名？

(3)、已知 $y ⩾ 245$ ， $z ⩾ 245$ ，求高三年级中女生比男生多的概率.

查看试题解析

试验田	试验田1	试验田2	试验田3	试验田4	试验田5
死亡数	23	32	24	29	17

鞋码	$35$	$36$	$37$	$38$	$39$	$40$	$41$	$42$	$43$	$44$	合计
男生			$3$	$6$	$8$	$11$	$12$	$6$	$7$	$2$	$55$
女生	$4$	$6$	$12$	$9$	$9$	$2$	$2$			$1$	$45$

	高一年级	高二年级	高三年级
女生	373	x	y
男生	377	370	z