备考2020年高考数学一轮复习：58 排列与组合（理科专用）

试卷更新日期：2019-11-05 类型：一轮复习

进入出卷网下载

一、单选题

1. $18 \times 17 \times 16 \times \dots \times 12 \times 11$ 等于（）

A、 $A_{18}^{8}$ B、 $A_{18}^{9}$ C、 $A_{18}^{10}$ D、 $A_{18}^{11}$

查看试题解析
2. 自2020年起,高考成绩由“ $3 + 3$ ”组成，其中第一个“3”指语文、数学、英语3科，第二个“3”指学生从物理、化学、生物、政治、历史、地理6科中任选3科作为选考科目，某同学计划从物理、化学、生物3科中任选两科，从政治、历史、地理3科中任选1科作为选考科目，则该同学3科选考科目的不同选法的种数为（）

A、6 B、7 C、8 D、9

查看试题解析
3. 已知有穷数列 ${a_{n}} (n = 1 ，$ 2，3， $\dots$ ， $6}$ 满足 $a_{n} \in (1 ，$ 2，3， $\dots$ ， $10}$ ，且当 $i \neq j (i ， j = 1 ，$ 2，3， $\dots$ ， $6)$ 时， $a_{i} \neq a_{j} .$ 若 $a_{1} > a_{2} > a_{3}$ ，则符合条件的数列 ${a_{n}}$ 的个数是 $($ $)$

A、 $C_{10}^{3} A_{7}^{3}$ B、 $C_{10}^{3} C_{10}^{3}$ C、 $A_{10}^{3} A_{7}^{3}$ D、 $C_{10}^{6} A_{6}^{3}$

查看试题解析
4. 学校新入职的5名教师要参加由市教育局组织的暑期3期上岗培训，每人只参加其中1期培训，每期至多派2人，由于时间上的冲突，甲教师不能参加第一期培训，则学校不同的选派方法有（）

A、 $84$ 种 B、 $60$ 种 C、 $42$ 种 D、 $36$ 种

查看试题解析
5. 《中国诗词大会》（第二季)亮点颇多，十场比赛每场都有一首特别设计的开场诗词，在声光舞美的配合下，百人团齐声朗诵，别有韵味.若《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场，且《将进酒》排在《望岳》的前面，《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后，则后六场的排法有（）

A、144种 B、288种 C、360种 .720种

查看试题解析
6. 将4名志愿者分别安排到火车站、轮渡码头、机场工作，要求每一个地方至少安排一名志愿者，其中甲、乙两名志愿者不安排在同一个地方工作，则不同的安排方法共有（）

A、24种 B、30种 C、32种 D、36种

查看试题解析
7. 在某班进行的歌唱比赛中，共有5位选手参加，其中3位女生，2位男生．如果2位男生不能连着出场，且女生甲不能排在第一个，那么出场顺序的排法种数为（）

A、30 B、36 C、60 D、72

查看试题解析
8. 有三个兴趣小组，甲、乙两位同学各自参加其中的一个小组，每位同学参加各个小组的可能性相同，则这两位同学不在同一个兴趣小组的情况有（）种

A、3 B、6 C、9 D、12

查看试题解析
9. 如图，花坛内有五个花池，有五种不同颜色的花卉可供栽种，每个花池内只能种同种颜色的花卉，相邻两池的花色不同，则最多有几种栽种方案（）

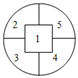A、180种 B、240种 C、360种 D、420种

查看试题解析
10. 6人站成一排，甲、乙、丙三人必须站在一起的排列种数为（）

A、18 B、72 C、36 D、144

查看试题解析
11. 篮球比赛中每支球队的出场阵容由5名队员组成，2017年的 $N B A$ 篮球赛中，休斯敦火箭队采取了“八人轮换”的阵容，即每场比赛只有8名队员有机会出场，这8名队员中包含两名中锋，两名控球后卫，若要求每一套出场阵容中有且仅有一名中锋，至少包含一名控球后卫，则休斯敦火箭队的主教练一共有（）种出场阵容的选择.

A、16 B、28 C、84 D、96

查看试题解析
12. 中国有十二生肖，又叫十二属相，每一个人的出生年份对应了十二种动物（鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪）中的一种，现有十二生肖的吉祥物各一个，三位同学依次选一个作为礼物，甲同学喜欢牛和马，乙同学喜欢牛、狗和羊，丙同学哪个吉祥物都喜欢，如果让三位同学选取礼物都满意，则选法有（）

A、30种 B、50种 C、60种 D、90种

查看试题解析

二、填空题

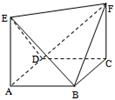
13. 定义“规范01数列” ${a_{n}}$ 如下： ${a_{n}}$ 共有 $2 m$ 项，其中 $m$ 项为0， $m$ 项为1，且对任意 $k \leq 2 m$ ， $a_{1} ， a_{2} ， \dots ， a_{k}$ 中0的个数不少于1的个数.若 $m = 4$ ，则不同的“规范01数列”共有个。

查看试题解析
14. 有 $n$ 个元素的集合的3元子集共有20个，则 $n$ = .

查看试题解析
15. 已知有7把椅子摆成一排，现有3人随机就座，那么任何两人不相邻的坐法种数为.（请用数字作答）

查看试题解析
16. 江苏省高中生进入高二年级时需从“物理、化学、生物、历史、地理、政治、艺术”科目中选修若干进行分科，分科规定如下：从物理和历史中选择一门学科后再从化学、生物、地理、政治中选择两门学科作为一种组合，或者只选择艺术这门学科，则共有种不同的选课组合.（用数字作答）

查看试题解析
17. 从1，3，5三个数中选两个数字，从0，2两个数中选一个数字，组成没有重复数字的三位数，其中奇数的个数为.

查看试题解析
18. 如图所示的几何体ABCDEF中，ABCD是平行四边形且AE∥CF，六个顶点任意两点连线能组成异面直线的对数是

查看试题解析

三、解答题

19. 一个口袋里装有7个白球和1个红球，从口袋中任取5个球．

(1)、共有多少种不同的取法？

(2)、其中恰有一个红球，共有多少种不同的取法？

(3)、其中不含红球，共有多少种不同的取法？

查看试题解析
20. 某兴趣小组有9名学生．若从9名学生中选取3人，则选取的3人中恰好有一个女生的概率是 $\frac{15}{28}$ ．

(1)、该小组中男女学生各多少人？

(2)、9个学生站成一列队，现要求女生保持相对顺序不变（即女生前后顺序保持不变）重新站队，问有多少种重新站队的方法？（要求用数字作答）

(3)、9名学生站成一列，要求男生必须两两站在一起，有多少种站队的方法？（要求用数字作答）

查看试题解析
21. 按下列要求分配6本不同的书,各有多少种不同的分配方式?

(1)、分成三份,1份1本,1份2本,1份3本;

(2)、甲、乙、丙三人中,一人得1本,一人得2本,一人得3本;

(3)、平均分成三份,每份2本;

(4)、平均分配给甲、乙、丙三人,每人2本;

(5)、分成三份,1份4本,另外两份每份1本;

(6)、甲、乙、丙三人中,一人得4本,另外两人每人得1本;

查看试题解析