备考2020年高考数学一轮复习：57 分类加法计数原理与分步乘法计数原理（理科专用）

试卷更新日期：2019-11-05 类型：一轮复习

进入出卷网下载

一、单选题

1. 完成一项工作，有两种方法，有5个人只会用第一种方法，另外有4个人只会用第二种方法，从这9个人中选1个人完成这项工作，则不同的选法共有（）

A、5种 B、4种 C、9种 D、20种

查看试题解析
2. 如图所示十字路口来往的车辆，如果不允许回头，共有不同的行车路线有（）

A、24种 B、16种 C、12种 D、10种

查看试题解析
3. 用10元、5元和1元来支付20元钱的书款，不同的支付方法的种数为（）

A、3 B、5 C、9 D、12

查看试题解析
4. 某一数学问题可用综合法和分析法两种方法证明，有5位同学只会用综合法证明，有3位同学只会用分析法证明，现任选1名同学证明这个问题，不同的选法种数有（）种．

A、8 B、15 C、18 D、30

查看试题解析

5. 根据新高考改革方案，某地高考由文理分科考试变为“3+3”模式考试．某学校为了解高一年425名学生选课情况，在高一年下学期进行模拟选课，统计得到选课组合排名前4种如下表所示，其中物理、化学、生物为理科，政治、历史、地理为文科，“√”表示选择该科，“×”表示未选择该科，根据统计数据，下列判断错误的是（）

学科人数	物理	化学	生物	政治	历史	地理
124	√	√	×	×	×	√
101	×	×	√	×	√	√
86	×	√	√	×	×	√
74	√	×	√	×	√	×

A、前4种组合中，选择生物学科的学生更倾向选择两理一文组合 B、前4种组合中，选择两理一文的人数多于选择两文一理的人数 C、整个高一年段，选择地理学科的人数多于选择其他任一学科的人数 D、整个高一年段，选择物理学科的人数多于选择生物学科的人数

查看试题解析

6. 如图，给7条线段的5个端点涂色，要求同一条线段的两个端点不能同色，现有4种不同的颜色可供选择，则不同的涂色方法种数有（）

A、24 B、48 C、96 D、120

查看试题解析
7. 牡丹江一中2019年将实行新课程改革，即除语、数、外三科为必考科目外，还要在理、化、生、史、地、政六科中选择三科作为选考科目．已知某生的高考志愿为北京大学环境科学专业，按照17年北大高考招生选考科目要求物、化必选，为该生安排课表（上午四节、下午四节，上午第四节和下午第一节不算相邻），现该生某天最后两节为自习课，且数学不排下午第一节，语文、外语不相邻，则该生该天课表有（）种．

A、444 B、1776 C、1440 D、1560

查看试题解析
8. $2020$ 年东京夏季奥运会将设置 $4 \times 100$ 米男女混合泳接力这一新的比赛项目，比赛的规则是：每个参赛国家派出2男2女共计4名运动员比赛，按照仰泳 $\to$ 蛙泳 $\to$ 蝶泳 $\to$ 自由泳的接力顺序，每种泳姿 $100$ 米且由一名运动员完成，每个运动员都要出场. 现在中国队确定了备战该项目的4名运动员名单，其中女运动员甲只能承担仰泳或者自由泳，男运动员乙只能承担蝶泳或自由泳，剩下的男女各一名运动员则四种泳姿都可以上，那么中国队共有（）种兵布阵的方式.

A、 $6$ B、 $12$ C、 D、

查看试题解析
9. 现有5项工程由甲、乙、丙3个工程队承包，每队至少一项，但甲承包的项目不超过2个，不同的承包方案有（）种

A、130 B、150 C、220 D、240

查看试题解析
10. 从1，3，5三个数中选两个数字，从0，2两个数中选一个数字，组成没有重复数字的三位数，其中奇数的个数为（）

A、6 B、12 C、18 D、24

查看试题解析
11. 如图，用4种不同的颜色涂入图中的矩形A ， B ， C ， D中，要求相邻的矩形涂色不同，则不同的涂法有（）

A、72种 B、48种 C、24种 D、12种

查看试题解析

二、填空题

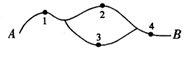
12. 五一假期从5月1日至4日调休4天，某班6名同学准备五一期间去参加社会实践做志愿者，每人社会实践一天，且甲乙两人不在同一天的不同安排方案有种（用数字作答）．

查看试题解析
13. 用1、2、3、4、5、6组成没有重复数字的六位数，要求任何相邻两个数字的奇偶性不同，这样的六位数的个数是（用数字作答）.

查看试题解析
14. 如图，在A、B间有四个焊接点，若焊接点脱落，而可能导致电路不通，如今发现A、B之间线路不通，则焊接点脱落的不同情况有种．

查看试题解析
15. 已知集合 $A = {(x, y) | 1 \leq x \leq 4, 1 \leq y \leq 4, x, y \in N}$ ，现从集合 $A$ 中任意取出三个点，以这三个点为顶点能够得到个不同的直角三角形．

查看试题解析
16. 如图，有7个白色正方形方块排成一列，现将其中4块涂上黑色，规定从左往右数，无论数到第几块，黑色方块总不少于白色方块的涂法有种。

查看试题解析
17. 在一个正六边形的6个区域栽种观赏植物，如图，要求同一块中种同一种植物，相邻的两块种不同的植物。现有4种不同的植物可供选择，则共有种不同的栽种方案?

查看试题解析
18. 某种型号的机器人组装由 $A ， B ， C ， D$ 四道工序，完成它们需要的时间依次为 $5 ， x ， 3 ， 3$ 小时，已知完成这四道工序先后顺序及相互关系是：① $A ， B$ 可以同时开工；②只有在 $B$ 完成后 $C$ 才能开工；③只有在 $A ， C$ 都完成后 $D$ 才能开工.若完成该型号的机器人组装总时间为9小时，则完成工序 $B$ 需要的时间的最大值为．

查看试题解析

三、解答题

19. 5名男生3名女生参加升旗仪式：

(1)、站两横排，3名女生站前排，5名男生站后排有多少种站法？

(2)、站两纵列，每列4人，每列都有女生且女生站在男生前面，有多少种排列方法？

查看试题解析
20. 某次文艺晚会上共演出7个节目，其中2个歌曲，3个舞蹈，2个曲艺节目，求分别满足下列条件的节自编排方法有多少种？（用数字作答）

(1)、一个歌曲节目开头，另个歌曲节目放在最后压台；

(2)、2个歌曲节目相邻且2个曲艺节目不相邻．

查看试题解析
21. 对于给定的大于1的正整数n，设 $x = a_{0} + a_{1} n + a_{2} n^{2} + \dots + a_{n} n^{n}$ ，其中 $a_{i} \in {0 ， 1 ， 2 ， \dots ， n - 1} ， i = 0 ， 1 ， 2 ， \dots ， n$ ，且 $a_{n} \neq 0 ，$ 记满足条件的所有x的和为 $A_{n}$ ，

(1)、求 $A_{2}$

(2)、设 $A_{n} = \frac{n^{n} (n - 1)}{2} f (n)$ ，求 $f (n)$

查看试题解析