湖北省黄石市下陆区2019-2020学年八年级上学期数学10月月考试卷
试卷更新日期:2019-11-04 类型:月考试卷
一、单选题
-
1. 以下列各组线段为边,能组成三角形的是( )A、2cm,3cm,5cm B、5cm,6cm,10cm C、1cm,1cm,3cm D、3cm,4cm,9cm2. 为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是( )
 A、两点之间,线段最短 B、垂线段最短 C、三角形具有稳定性 D、两直线平行,内错角相等3. 如果正多边形的一个内角是 ,则这个多边形是( )A、正十边形 B、正九边形 C、正八边形 D、正七边形4. 已知 中, 是 的 倍, 比 大 ,则 等于( )A、 B、 C、 D、5. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.
A、两点之间,线段最短 B、垂线段最短 C、三角形具有稳定性 D、两直线平行,内错角相等3. 如果正多边形的一个内角是 ,则这个多边形是( )A、正十边形 B、正九边形 C、正八边形 D、正七边形4. 已知 中, 是 的 倍, 比 大 ,则 等于( )A、 B、 C、 D、5. 如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带( )去.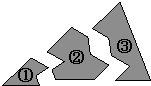 A、① B、② C、③ D、①和②6. 一定能确定△ABC≌△DEF的条件是( )
A、① B、② C、③ D、①和②6. 一定能确定△ABC≌△DEF的条件是( )
A、∠A=∠D,AB=DE,∠B=∠E B、∠A=∠E,AB=EF,∠B=∠D C、A B=DE,BC=EF,∠A=∠D D、∠A=∠D,∠B=∠E,∠C=∠F7. 以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边,可以画出三角形的个数是( )A、1个 B、2个 C、3个 D、4个8. 在等腰△ABC中,AB=AC,一腰上的中线BD将这个三角形的周长分为15和12两部分,则这个等腰三角形的底边长为( )A、7 B、7或11 C、11 D、7或109. 下面四个图形中,线段BD是△ABC的高的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
10. 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )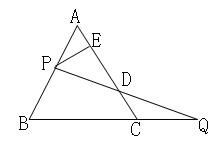 A、 B、 C、 D、不能确定
A、 B、 C、 D、不能确定二、填空题
-
11. 如图, 为 中 边的延长线上一点, ,则 度.
 12. 等腰三角形一边长为 ,周长 ,则腰长是.13. 在等腰三角形中,有一个角是 ,它的一条腰上的高与底边的夹角是.14. 如图,小亮从 点出发,沿直线前进 后向左转 交再沿直线前进 ,又向左转 ,照这样走下去,他第一次回到出发地 点时,一共走了 .
12. 等腰三角形一边长为 ,周长 ,则腰长是.13. 在等腰三角形中,有一个角是 ,它的一条腰上的高与底边的夹角是.14. 如图,小亮从 点出发,沿直线前进 后向左转 交再沿直线前进 ,又向左转 ,照这样走下去,他第一次回到出发地 点时,一共走了 . 15. 如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=度.
15. 如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=度. 16. 如图, 是 的中线, 是 的中线, 是 的中线,如果 的面积是 .那么 △ABC的面积 为.
16. 如图, 是 的中线, 是 的中线, 是 的中线,如果 的面积是 .那么 △ABC的面积 为.
三、解答题
-
17. 如图,在△ABC中,∠B=30°,∠ACE=35°,CE平分∠ACB,求∠A的度数
 18. 如图,已知AD、BC相交于点O,AB=CD,AD=CB.求证:∠A=∠C.
18. 如图,已知AD、BC相交于点O,AB=CD,AD=CB.求证:∠A=∠C. 19. 已知:如图,C是线段AB的中点,∠A=∠B,∠ACE=∠BCD.
19. 已知:如图,C是线段AB的中点,∠A=∠B,∠ACE=∠BCD.求证:AD=BE.
 20. 如图,已知 ,点 分别在 轴正半轴和 轴正半轴上, ,试求 的值.
20. 如图,已知 ,点 分别在 轴正半轴和 轴正半轴上, ,试求 的值. 21. 如图,四边形 中, , 平分 平分 交于 点.
21. 如图,四边形 中, , 平分 平分 交于 点. (1)、求证: ;(2)、求证: .22. 如图: 是 的高, 为 上一点, 交 于 ,且有 .求证: .
(1)、求证: ;(2)、求证: .22. 如图: 是 的高, 为 上一点, 交 于 ,且有 .求证: . 23. 如图,在 中, ,点 是 的中点, 于 交 于 交 的延长线于 .
23. 如图,在 中, ,点 是 的中点, 于 交 于 交 的延长线于 .
求证:
(1)、 ;(2)、 垂直平分 .24. 如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.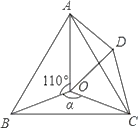 (1)、求证:△OCD是等边三角形;(2)、当α=150°时,试判断△AOD的形状,并说明理由;(3)、探究:当α为多少度时,△AOD是等腰三角形.25. 如图,A(-t,0)、B(0,t),其中t>0,点C为OA上一点,OD⊥BC于点D,且∠BCO=45°+∠COD
(1)、求证:△OCD是等边三角形;(2)、当α=150°时,试判断△AOD的形状,并说明理由;(3)、探究:当α为多少度时,△AOD是等腰三角形.25. 如图,A(-t,0)、B(0,t),其中t>0,点C为OA上一点,OD⊥BC于点D,且∠BCO=45°+∠COD
 (1)、求证:BC平分∠ABO(2)、求 的值(3)、若点P为第三象限内一动点,且∠APO=135°,试问AP和BP是否存在某种确定的位置关系?说明理由
(1)、求证:BC平分∠ABO(2)、求 的值(3)、若点P为第三象限内一动点,且∠APO=135°,试问AP和BP是否存在某种确定的位置关系?说明理由