辽宁省锦州市2019年中考数学试卷
试卷更新日期:2019-11-04 类型:中考真卷
一、单选题
-
1. ﹣2019的相反数是( )A、 B、﹣ C、2019 D、﹣20192. 下列既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 甲、乙、丙、丁四名同学进行跳高测试,每人10次跳高成绩的平均数都是1.28m,方差分别是s甲2=0.60,s乙2=0.62,s丙2=0.58,s丁2=0.45,则这四名同学跳高成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁4. 下列运算正确的是( )A、x ÷x =x B、(﹣x ) =x C、4x +3x =7x D、(x+y) =x +y5. 如图,AC与BD交于点O,AB∥CD,∠AOB=105°,∠B=30°,则∠C的度数为( )
3. 甲、乙、丙、丁四名同学进行跳高测试,每人10次跳高成绩的平均数都是1.28m,方差分别是s甲2=0.60,s乙2=0.62,s丙2=0.58,s丁2=0.45,则这四名同学跳高成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁4. 下列运算正确的是( )A、x ÷x =x B、(﹣x ) =x C、4x +3x =7x D、(x+y) =x +y5. 如图,AC与BD交于点O,AB∥CD,∠AOB=105°,∠B=30°,则∠C的度数为( )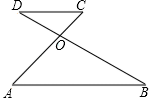 A、45° B、55° C、60° D、75°6. 如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为( )
A、45° B、55° C、60° D、75°6. 如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为( )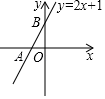 A、 B、 C、2 D、47. 在矩形ABCD中,AB=3,BC=4,M是对角线BD上的动点,过点M作ME⊥BC于点E,连接AM,当△ADM是等腰三角形时,ME的长为( )A、 B、 C、 或 D、 或8. 如图,在菱形ABCD中,∠B=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿折线BA→AC运动到点C,同时动点Q从点A出发,以相同速度沿折线AC→CD运动到点D,当一个点停止运动时,另一个点也随之停止.设△APQ的面积为y,运动时间为x秒,则下列图象能大致反映y与x之间函数关系的是( )
A、 B、 C、2 D、47. 在矩形ABCD中,AB=3,BC=4,M是对角线BD上的动点,过点M作ME⊥BC于点E,连接AM,当△ADM是等腰三角形时,ME的长为( )A、 B、 C、 或 D、 或8. 如图,在菱形ABCD中,∠B=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿折线BA→AC运动到点C,同时动点Q从点A出发,以相同速度沿折线AC→CD运动到点D,当一个点停止运动时,另一个点也随之停止.设△APQ的面积为y,运动时间为x秒,则下列图象能大致反映y与x之间函数关系的是( )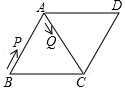 A、
A、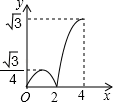 B、
B、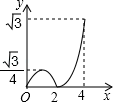 C、
C、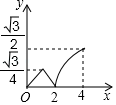 D、
D、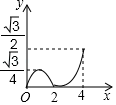
二、填空题
-
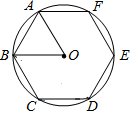
9. 在函数y= 中,自变量x的取值范围是 .10. 为了落实“优化税收营商环境,助力经济发展和民生改善”的政策,国家税务总局统计数据显示,2018年5至10月合计减税2980亿元,将2980亿元用科学记数法表示为元.11. 在一个不透明的袋子中装有3个白球和若干个红球,这些球除颜色外都相同.每次从袋子中随机摸出一个球,记下颜色后再放回袋中,通过多次重复试验发现摸出红球的频率稳定在0.7附近,则袋子中红球约有个.12. 如图,正六边形ABCDEF内接于⊙O,边长AB=2,则扇形AOB的面积为.
 13. 甲、乙两地相距1000km,如果乘高铁列车从甲地到乙地比乘特快列车少用3h,已知高铁列车的平均速度是特快列车的1.6倍,设特快列车的平均速度为xkm/h,根据题意可列方程为.14. 如图,将一个含30°角的三角尺ABC放在直角坐标系中,使直角顶点C与原点O重合,顶点A,B分别在反比例函数y=﹣ 和y= 的图象上,则k的值为.
13. 甲、乙两地相距1000km,如果乘高铁列车从甲地到乙地比乘特快列车少用3h,已知高铁列车的平均速度是特快列车的1.6倍,设特快列车的平均速度为xkm/h,根据题意可列方程为.14. 如图,将一个含30°角的三角尺ABC放在直角坐标系中,使直角顶点C与原点O重合,顶点A,B分别在反比例函数y=﹣ 和y= 的图象上,则k的值为.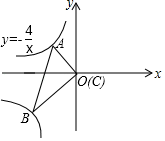 15. 如图,在矩形ABCD中,AB=3,BC=2,M是AD边的中点,N是AB边上的动点,将△AMN沿MN所在直线折叠,得到△A′MN,连接A′C,则A′C的最小值是.
15. 如图,在矩形ABCD中,AB=3,BC=2,M是AD边的中点,N是AB边上的动点,将△AMN沿MN所在直线折叠,得到△A′MN,连接A′C,则A′C的最小值是.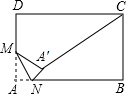 16. 如图,边长为4的等边△ABC,AC边在x轴上,点B在y轴的正半轴上,以OB为边作等边△OBA1 , 边OA1与AB交于点O1 , 以O1B为边作等边△O1BA2 , 边O1A2与A1B交于点O2 , 以O2B为边作等边△O2BA3 , 边O2A3与A2B交于点O3 , …,依此规律继续作等边△On﹣1BAn , 记△OO1A的面积为S1 , △O1O2A1的面积为S2 , △O2O3A2的面积为S3 , …,△On﹣1OnAn﹣1的面积为Sn , 则Sn=.(n≥2,且n为整数)
16. 如图,边长为4的等边△ABC,AC边在x轴上,点B在y轴的正半轴上,以OB为边作等边△OBA1 , 边OA1与AB交于点O1 , 以O1B为边作等边△O1BA2 , 边O1A2与A1B交于点O2 , 以O2B为边作等边△O2BA3 , 边O2A3与A2B交于点O3 , …,依此规律继续作等边△On﹣1BAn , 记△OO1A的面积为S1 , △O1O2A1的面积为S2 , △O2O3A2的面积为S3 , …,△On﹣1OnAn﹣1的面积为Sn , 则Sn=.(n≥2,且n为整数)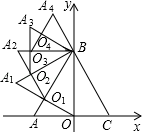
三、解答题
-
17. 先化简,再求值:( ﹣1) ,其中a=(π﹣ )0+( )﹣1.18. 为了响应“学习强国,阅读兴辽”的号召,某校鼓励学生利用课余时间广泛阅读,学校打算购进一批图书.为了解学生对图书类别的喜欢情况,校学生会随机抽取部分学生进行问卷调查,规定被调查学生从“文学、历史、科学、生活”中只选择自己最喜欢的一类,根据调查结果绘制了下面不完整的统计图.

请根据图表信息,解答下列问题.
(1)、此次共调查了学生多少人;(2)、请通过计算补全条形统计图;(3)、若该校共有学生2200人,请估计这所学校喜欢“科学”类书的学生人数.19. 对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的A,B,C,D四个小区进行检查,并且每个小区不重复检查.(1)、甲组抽到A小区的概率是多少(2)、请用列表或画树状图的方法求甲组抽到A小区,同时乙组抽到C小区的概率.20. 某市政部门为了保护生态环境,计划购买A,B两种型号的环保设备.已知购买一套A型设备和三套B型设备共需230万元,购买三套A型设备和两套B型设备共需340万元.(1)、求A型设备和B型设备的单价各是多少万元;(2)、根据需要市政部门采购A型和B型设备共50套,预算资金不超过3000万元,问最多可购买A型设备多少套?21. 如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上,求旗杆AB的高度.(结果精确到0.1m,参考数据: ≈1.41, =1.73) 22. 如图,M,N是以AB为直径的⊙O上的点,且 = ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
22. 如图,M,N是以AB为直径的⊙O上的点,且 = ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F. (1)、求证:MF是⊙O的切线;(2)、若CN=3,BN=4,求CM的长.23. 2019年在法国举办的女足世界杯,为人们奉献了一场足球盛宴.某商场销售一批足球文化衫,已知该文化衫的进价为每件40元,当售价为每件60元时,每个月可售出100件.根据市场行情,现决定涨价销售,调查表明,每件商品的售价每上涨1元,每个月会少售出2件,设每件商品的售价为x元,每个月的销量为y件.(1)、求y与x之间的函数关系式;(2)、当每件商品的售价定为多少元时,每个月的利润恰好为2250元;(3)、当每件商品的售价定为多少元时,每个月获得利润最大?最大月利润为多少?24. 已知,在Rt△ABC中,∠ACB=90°,D是BC边上一点,连接AD,分别以CD和AD为直角边作Rt△CDE和Rt△ADF,使∠DCE=∠ADF=90°,点E,F在BC下方,连接EF.
(1)、求证:MF是⊙O的切线;(2)、若CN=3,BN=4,求CM的长.23. 2019年在法国举办的女足世界杯,为人们奉献了一场足球盛宴.某商场销售一批足球文化衫,已知该文化衫的进价为每件40元,当售价为每件60元时,每个月可售出100件.根据市场行情,现决定涨价销售,调查表明,每件商品的售价每上涨1元,每个月会少售出2件,设每件商品的售价为x元,每个月的销量为y件.(1)、求y与x之间的函数关系式;(2)、当每件商品的售价定为多少元时,每个月的利润恰好为2250元;(3)、当每件商品的售价定为多少元时,每个月获得利润最大?最大月利润为多少?24. 已知,在Rt△ABC中,∠ACB=90°,D是BC边上一点,连接AD,分别以CD和AD为直角边作Rt△CDE和Rt△ADF,使∠DCE=∠ADF=90°,点E,F在BC下方,连接EF.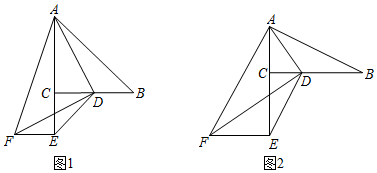 (1)、如图1,当BC=AC,CE=CD,DF=AD时,
(1)、如图1,当BC=AC,CE=CD,DF=AD时,求证:①∠CAD=∠CDF,
②BD=EF;
(2)、如图2,当BC=2AC,CE=2CD,DF=2AD时,猜想BD和EF之间的数量关系?并说明理由.25. 如图1,在平面直角坐标系中,一次函数y=﹣ x+3的图象与x轴交于点A,与y轴交于B点,抛物线y=﹣x2+bx+c经过A,B两点,在第一象限的抛物线上取一点D,过点D作DC⊥x轴于点C,交直线AB于点E.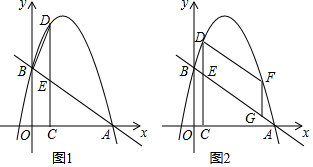 (1)、求抛物线的函数表达式(2)、是否存在点D,使得△BDE和△ACE相似?若存在,请求出点D的坐标,若不存在,请说明理由;(3)、如图2,F是第一象限内抛物线上的动点(不与点D重合),点G是线段AB上的动点.连接DF,FG,当四边形DEGF是平行四边形且周长最大时,请直接写出点G的坐标.
(1)、求抛物线的函数表达式(2)、是否存在点D,使得△BDE和△ACE相似?若存在,请求出点D的坐标,若不存在,请说明理由;(3)、如图2,F是第一象限内抛物线上的动点(不与点D重合),点G是线段AB上的动点.连接DF,FG,当四边形DEGF是平行四边形且周长最大时,请直接写出点G的坐标.