辽宁省抚顺市2019年中考数学试卷
试卷更新日期:2019-11-04 类型:中考真卷
一、单选题
-
1. 3的相反数是( )A、 3 B、-3 C、 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是由5个小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方块的个数,则这个几何体的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 一组数据1,3, ,3,4的中位数是( )A、1 B、 C、 D、36. 下列调查中,最适合采用全面调查的是( )A、对全国中学生视力和用眼卫生情况的调查 B、对某班学生的身高情况的调查 C、对某鞋厂生产的鞋底能承受的弯折次数的调查 D、对某池塘中现有鱼的数量的调查7. 若一个等腰三角形的两边长分别为2,4,则第三边的长为( )A、2 B、3 C、4 D、2或48. 一副直角三角尺如图摆放,点 在 的延长线上, , , , ,则∠ 的度数是( )
5. 一组数据1,3, ,3,4的中位数是( )A、1 B、 C、 D、36. 下列调查中,最适合采用全面调查的是( )A、对全国中学生视力和用眼卫生情况的调查 B、对某班学生的身高情况的调查 C、对某鞋厂生产的鞋底能承受的弯折次数的调查 D、对某池塘中现有鱼的数量的调查7. 若一个等腰三角形的两边长分别为2,4,则第三边的长为( )A、2 B、3 C、4 D、2或48. 一副直角三角尺如图摆放,点 在 的延长线上, , , , ,则∠ 的度数是( )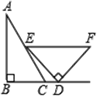 A、 B、 C、 D、9. 如图, , 是四边形 的对角线,点 , 分别是 , 的中点,点 , 分别是 , 的中点,连接 , , , ,要使四边形 为正方形,则需添加的条件是( )
A、 B、 C、 D、9. 如图, , 是四边形 的对角线,点 , 分别是 , 的中点,点 , 分别是 , 的中点,连接 , , , ,要使四边形 为正方形,则需添加的条件是( ) A、 , B、 , C、 , D、 ,10. 如图,在等腰直角三角形 中, , , 是 边上的高,正方形 的边 在高 上, , 两点分别在 , 上.将正方形 以每秒 的速度沿射线 方向匀速运动,当点 与点 重合时停止运动.设运动时间为 ,正方形 与 重叠部分的面积为 ,则能反映 与 的函数关系的图象( )
A、 , B、 , C、 , D、 ,10. 如图,在等腰直角三角形 中, , , 是 边上的高,正方形 的边 在高 上, , 两点分别在 , 上.将正方形 以每秒 的速度沿射线 方向匀速运动,当点 与点 重合时停止运动.设运动时间为 ,正方形 与 重叠部分的面积为 ,则能反映 与 的函数关系的图象( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 据报道,某节日期间某市地铁二号线载客量达到17340000人次,再创历史新高.将数据17340000用科学记数法表示为.12. 不等式组 的解集是.13. 若关于 的一元二次方程 有两个实数根,则 的取值范围是.14. 如果把两条直角边长分别为5,10的直角三角形按相似比 进行缩小,得到的直角三角形的面积是.15. 一个小球在如图所示的方格地板上自由滚动,并随机停留在某块地板上,每块地板大小、质地完全相同,那么该小球停留在黑色区域的概率是.
 16. 如图,矩形 的顶点 , 在反比例函数 的图象上,若点 的坐标为 , , 轴,则点 的坐标为.
16. 如图,矩形 的顶点 , 在反比例函数 的图象上,若点 的坐标为 , , 轴,则点 的坐标为.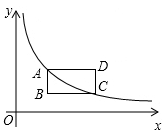 17. 如图,在 中, , , 是 所在平面内一点,以 , , , 为顶点的四边形是平行四边形,则 的长为.
17. 如图,在 中, , , 是 所在平面内一点,以 , , , 为顶点的四边形是平行四边形,则 的长为. 18. 如图,直线 的解析式是 ,直线 的解析式是 ,点 在 上, 的横坐标为 ,作 交 于点 ,点 在 上,以 , 为邻边在直线 , 间作菱形 ,分别以点 , 为圆心,以 为半径画弧得扇形 和扇形 ,记扇形 与扇形 重叠部分的面积为 ;延长 交 于点 ,点 在 上,以 , 为邻边在 , 间作菱形 ,分别以点 , 为圆心,以 为半径画弧得扇形 和扇形 ,记扇形 与扇形 重叠部分的面积为 按照此规律继续作下去,则 .(用含有正整数 的式子表示)
18. 如图,直线 的解析式是 ,直线 的解析式是 ,点 在 上, 的横坐标为 ,作 交 于点 ,点 在 上,以 , 为邻边在直线 , 间作菱形 ,分别以点 , 为圆心,以 为半径画弧得扇形 和扇形 ,记扇形 与扇形 重叠部分的面积为 ;延长 交 于点 ,点 在 上,以 , 为邻边在 , 间作菱形 ,分别以点 , 为圆心,以 为半径画弧得扇形 和扇形 ,记扇形 与扇形 重叠部分的面积为 按照此规律继续作下去,则 .(用含有正整数 的式子表示)
三、解答题
-
19. 先化简,再求值: ,其中 , .20. 为提升学生的艺术素养,某校计划开设四门选修课程:声乐、舞蹈、书法、摄影.要求每名学生必须选修且只能选修一门课程,为保证计划的有效实施,学校随机对部分学生进行了一次调查,并将调査结果绘制成如下不完整的统计表和统计图.
学生选修课程统计表
课程
人数
所占百分比
声乐
14
舞蹈
8
书法
16
摄影
合计

根据以上信息,解答下列问题:
(1)、 , .(2)、求出 的值并补全条形统计图.(3)、该校有1500名学生,请你估计选修“声乐”课程的学生有多少名.(4)、七(1)班和七(2)班各有2人选修“舞蹈”课程且有舞蹈基础,学校准备从这4人中随机抽取2人编排“舞蹈”在开班仪式上表演,请用列表法或画树状图的方法求所抽取的2人恰好来自同一个班级的概率.21. 为响应“绿色生活,美丽家园”号召,某社区计划种植甲、乙两种花卉来美化小区环境.若种植甲种花卉 ,乙种花卉 ,共需430元;种植甲种花卉 ,乙种花卉 ,共需260元.(1)、求:该社区种植甲种花卉 和种植乙种花卉 各需多少元?(2)、该社区准备种植两种花卉共 且费用不超过6300元,那么社区最多能种植乙种花卉多少平方米?22. 如图,在 中, , ,点 在 的内部, 经过 , 两点,交 于点 ,连接 并延长交 于点 ,以 , 为邻边作 . (1)、判断 与 的位置关系,并说明理由.(2)、若点 是 的中点, 的半径为2,求 的长.23. 如图,学校教学楼上悬挂一块长为 的标语牌,即 .数学活动课上,小明和小红要测量标语牌的底部点 到地面的距离.测角仪支架高 ,小明在 处测得标语牌底部点 的仰角为 ,小红在 处测得标语牌顶部点 的仰角为 , ,依据他们测量的数据能否求出标语牌底部点 到地面的距离 的长?若能,请计算;若不能,请说明理由(图中点 , , , , , , 在同一平面内)
(1)、判断 与 的位置关系,并说明理由.(2)、若点 是 的中点, 的半径为2,求 的长.23. 如图,学校教学楼上悬挂一块长为 的标语牌,即 .数学活动课上,小明和小红要测量标语牌的底部点 到地面的距离.测角仪支架高 ,小明在 处测得标语牌底部点 的仰角为 ,小红在 处测得标语牌顶部点 的仰角为 , ,依据他们测量的数据能否求出标语牌底部点 到地面的距离 的长?若能,请计算;若不能,请说明理由(图中点 , , , , , , 在同一平面内)(参考数据: , ,
 24. 某网店销售一种儿童玩具,进价为每件30元,物价部门规定每件儿童玩具的销售利润不高于进价的 .在销售过程中发现,这种儿童玩具每天的销售量 (件 与销售单价 (元 满足一次函数关系.当销售单价为35元时,每天的销售量为350件;当销售单价为40元时,每天的销售量为300件.(1)、求 与 之间的函数关系式.(2)、当销售单价为多少时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是多少?25. 如图,点 , 分别在正方形 的边 , 上,且 ,点 在射线 上(点 不与点 重合).将线段 绕点 顺时针旋转 得到线段 ,过点 作 的垂线 ,垂足为点 ,交射线 于点 .
24. 某网店销售一种儿童玩具,进价为每件30元,物价部门规定每件儿童玩具的销售利润不高于进价的 .在销售过程中发现,这种儿童玩具每天的销售量 (件 与销售单价 (元 满足一次函数关系.当销售单价为35元时,每天的销售量为350件;当销售单价为40元时,每天的销售量为300件.(1)、求 与 之间的函数关系式.(2)、当销售单价为多少时,该网店销售这种儿童玩具每天获得的利润最大,最大利润是多少?25. 如图,点 , 分别在正方形 的边 , 上,且 ,点 在射线 上(点 不与点 重合).将线段 绕点 顺时针旋转 得到线段 ,过点 作 的垂线 ,垂足为点 ,交射线 于点 .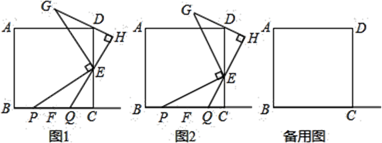 (1)、如图1,若点 是 的中点,点 在线段 上,线段 , , 的数量关系为.(2)、如图2,若点 不是 的中点,点 在线段 上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.(3)、正方形 的边长为6, , ,请直接写出线段 的长.26. 如图,抛物线 与 轴交于 , 两点,与 轴交于点 ,点 是抛物线的顶点.
(1)、如图1,若点 是 的中点,点 在线段 上,线段 , , 的数量关系为.(2)、如图2,若点 不是 的中点,点 在线段 上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.(3)、正方形 的边长为6, , ,请直接写出线段 的长.26. 如图,抛物线 与 轴交于 , 两点,与 轴交于点 ,点 是抛物线的顶点. (1)、求抛物线的解析式.(2)、点 是 轴负半轴上的一点,且 ,点 在对称轴右侧的抛物线上运动,连接 , 与抛物线的对称轴交于点 ,连接 ,当 平分 时,求点 的坐标.(3)、直线 交对称轴于点 , 是坐标平面内一点,请直接写出 与 全等时点 的坐标.
(1)、求抛物线的解析式.(2)、点 是 轴负半轴上的一点,且 ,点 在对称轴右侧的抛物线上运动,连接 , 与抛物线的对称轴交于点 ,连接 ,当 平分 时,求点 的坐标.(3)、直线 交对称轴于点 , 是坐标平面内一点,请直接写出 与 全等时点 的坐标.