辽宁省丹东市2019年中考数学试卷
试卷更新日期:2019-11-04 类型:中考真卷
一、单选题
-
1. ﹣2019的倒数是( )A、﹣2019 B、2019 C、﹣ D、2. 十年来,我国知识产权战略实施取得显著成就,全国著作权登记量已达到274.8万件.数据274.8万用科学记数法表示为( )A、2.748×102 B、274.8×104 C、2.748×106 D、0.2748×1073.
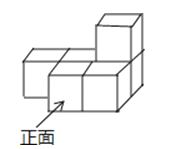
如图所示的几何体是由六个相同的小正方体组合而成的,它的俯视图是( )
 A、
A、 B、
B、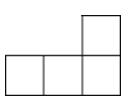 C、
C、 D、
D、 4. 下面计算正确的是( )A、3a﹣2a=1 B、2a2+4a2=6a4 C、(x3)2=x5 D、x8÷x2=x65. 如图,点C在∠AOB的边OA上,用尺规作出了CP∥OB,作图痕迹中, 是( )
4. 下面计算正确的是( )A、3a﹣2a=1 B、2a2+4a2=6a4 C、(x3)2=x5 D、x8÷x2=x65. 如图,点C在∠AOB的边OA上,用尺规作出了CP∥OB,作图痕迹中, 是( ) A、以点C为圆心、OD的长为半径的弧 B、以点C为圆心、DM的长为半径的弧 C、以点E为圆心、DM的长为半径的弧 D、以点E为圆心、OD的长为半径的弧6. 在从小到大排列的五个整数中,中位数是2,唯一的众数是4,则这五个数和的最大值是( )A、11 B、12 C、13 D、147. 等腰三角形一边长为2,它的另外两条边的长度是关于x的一元二次方程x2﹣6x+k=0的两个实数根,则k的值是 ( )A、8 B、9 C、8或9 D、128. 如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣2,0),对称轴为直线x=1.有以下结论:①abc>0;②8a+c>0;③若A(x1 , m),B(x2 , m)是抛物线上的两点,当x=x1+x2时,y=c;④点M,N是抛物线与x轴的两个交点,若在x轴下方的抛物线上存在一点P,使得PM⊥PN,则a的取值范围为a≥1;⑤若方程a(x+2)(4﹣x)=﹣2的两根为x1 , x2 , 且x1<x2 , 则﹣2≤x1<x2<4.其中结论正确的有( )
A、以点C为圆心、OD的长为半径的弧 B、以点C为圆心、DM的长为半径的弧 C、以点E为圆心、DM的长为半径的弧 D、以点E为圆心、OD的长为半径的弧6. 在从小到大排列的五个整数中,中位数是2,唯一的众数是4,则这五个数和的最大值是( )A、11 B、12 C、13 D、147. 等腰三角形一边长为2,它的另外两条边的长度是关于x的一元二次方程x2﹣6x+k=0的两个实数根,则k的值是 ( )A、8 B、9 C、8或9 D、128. 如图,二次函数y=ax2+bx+c(a≠0)的图象过点(﹣2,0),对称轴为直线x=1.有以下结论:①abc>0;②8a+c>0;③若A(x1 , m),B(x2 , m)是抛物线上的两点,当x=x1+x2时,y=c;④点M,N是抛物线与x轴的两个交点,若在x轴下方的抛物线上存在一点P,使得PM⊥PN,则a的取值范围为a≥1;⑤若方程a(x+2)(4﹣x)=﹣2的两根为x1 , x2 , 且x1<x2 , 则﹣2≤x1<x2<4.其中结论正确的有( )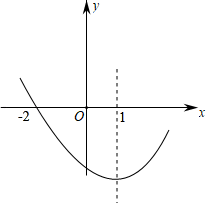 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
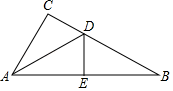
9. 分解因式2x3﹣8x2+8x=.10. 在函数y= 中,自变量x的取值范围是.11. 有5张无差别的卡片,上面分别标有﹣1,0, , ,π,从中随机抽取1张,则抽出的数是无理数的概率是.12. 关于x的不等式组 的解集是2<x<4,则a的值为.13. 如图,在△ABC中,∠C=90°,DE是AB的垂直平分线,AD恰好平分∠BAC.若DE=1,则BC的长是.
 14. 如图,点A在双曲线y= (x>0)上,过点A作AB⊥x轴于点B,点C在线段AB上且BC:CA=1:2,双曲线y= (x>0)经过点C,则k=.
14. 如图,点A在双曲线y= (x>0)上,过点A作AB⊥x轴于点B,点C在线段AB上且BC:CA=1:2,双曲线y= (x>0)经过点C,则k=.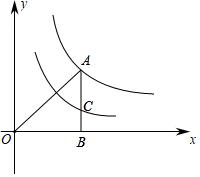 15. 如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为.
15. 如图,在平面直角坐标系中,点A,C分别在x轴、y轴上,四边形ABCO是边长为4的正方形,点D为AB的中点,点P为OB上的一个动点,连接DP,AP,当点P满足DP+AP的值最小时,直线AP的解析式为.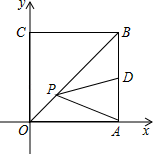 16. 如图,在平面直角坐标系中,OA=1,以OA为一边,在第一象限作菱形OAA1B,并使∠AOB=60°,再以对角线OA1为一边,在如图所示的一侧作相同形状的菱形OA1A2B1 , 再依次作菱形OA2A3B2 , OA3A4B3 , ……,则过点B2018 , B2019 , A2019的圆的圆心坐标为.
16. 如图,在平面直角坐标系中,OA=1,以OA为一边,在第一象限作菱形OAA1B,并使∠AOB=60°,再以对角线OA1为一边,在如图所示的一侧作相同形状的菱形OA1A2B1 , 再依次作菱形OA2A3B2 , OA3A4B3 , ……,则过点B2018 , B2019 , A2019的圆的圆心坐标为.
三、解答题
-
17. 先化简,再求代数式的值: ,其中x=3cos60°.18. 在下面的网格中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(﹣3,0),(﹣1,﹣1).

①请在图中画出平面直角坐标系,并直接写出点A的坐标.
②将△ABC绕着坐标原点顺时针旋转90°,画出旋转后的△A′B'C′.
③接写出在上述旋转过程中,点A所经过的路径长.
19. 为纪念“五四运动”100周年,某校举行了征文比赛,该校学生全部参加了比赛.比赛设置一等、二等、三等三个奖项,赛后该校对学生获奖情况做了抽样调查,并将所得数据绘制成如图所示的两幅不完整的统计图.根据图中信息解答下列问题: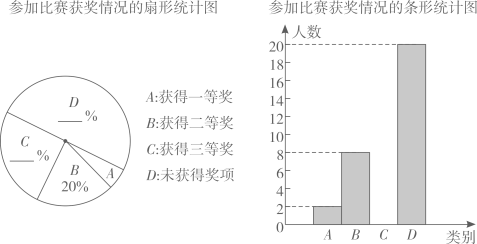 (1)、本次抽样调查学生的人数为.(2)、补全两个统计图,并求出扇形统计图中A所对应扇形圆心角的度数.(3)、若该校共有840名学生,请根据抽样调查结果估计获得三等奖的人数.20. 如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和4等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
(1)、本次抽样调查学生的人数为.(2)、补全两个统计图,并求出扇形统计图中A所对应扇形圆心角的度数.(3)、若该校共有840名学生,请根据抽样调查结果估计获得三等奖的人数.20. 如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和4等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘. (1)、利用画树状图或列表的方法,求甲获胜的概率.(2)、这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).21. 甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙两人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min.求乙到达科技馆时,甲离科技馆还有多远.22. 如图,在Rt△ABC中,∠ACB=90°,点D在AB上,以AD为直径的⊙O与边BC相切于点E,与边AC相交于点G,且 = ,连接GO并延长交⊙O于点F,连接BF.
(1)、利用画树状图或列表的方法,求甲获胜的概率.(2)、这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).21. 甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙两人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min.求乙到达科技馆时,甲离科技馆还有多远.22. 如图,在Rt△ABC中,∠ACB=90°,点D在AB上,以AD为直径的⊙O与边BC相切于点E,与边AC相交于点G,且 = ,连接GO并延长交⊙O于点F,连接BF.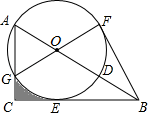 (1)、求证:①AO=AG.②BF是⊙O的切线.(2)、若BD=6,求图形中阴影部分的面积.23. 如图,在某街道路边有相距10m、高度相同的两盏路灯(灯杆垂直地面),小明为了测量路灯的高度,在地面A处测得路灯PQ的顶端仰角为14°,向前行走25m到达B处,在地面测得路灯MN的顶端仰角为24.3°,已知点A,B,Q,N在同一条直线上,请你利用所学知识帮助小明求出路灯的高度.(结果精确到0.1m.参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,sin24.3°≈0.41,cos24.3°≈0.91,tan24.3°≈0.45)
(1)、求证:①AO=AG.②BF是⊙O的切线.(2)、若BD=6,求图形中阴影部分的面积.23. 如图,在某街道路边有相距10m、高度相同的两盏路灯(灯杆垂直地面),小明为了测量路灯的高度,在地面A处测得路灯PQ的顶端仰角为14°,向前行走25m到达B处,在地面测得路灯MN的顶端仰角为24.3°,已知点A,B,Q,N在同一条直线上,请你利用所学知识帮助小明求出路灯的高度.(结果精确到0.1m.参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,sin24.3°≈0.41,cos24.3°≈0.91,tan24.3°≈0.45)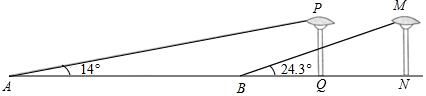 24. 某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.(1)、求出y与x的函数关系式,并写出自变量x的取值范围.(2)、当销售单价为多少元时,销售这种童装每月可获利1800元?(3)、当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?25. 已知:在△ABC外分别以AB,AC为边作△AEB与△AFC.
24. 某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.(1)、求出y与x的函数关系式,并写出自变量x的取值范围.(2)、当销售单价为多少元时,销售这种童装每月可获利1800元?(3)、当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?25. 已知:在△ABC外分别以AB,AC为边作△AEB与△AFC.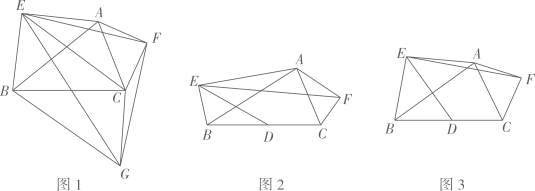 (1)、如图1,△AEB与△AFC分别是以AB,AC为斜边的等腰直角三角形,连接EF.以EF为直角边构造Rt△EFG,且EF=FG,连接BG,CG,EC.
(1)、如图1,△AEB与△AFC分别是以AB,AC为斜边的等腰直角三角形,连接EF.以EF为直角边构造Rt△EFG,且EF=FG,连接BG,CG,EC.求证:①△AEF≌△CGF;②四边形BGCE是平行四边形.
(2)、小明受到图1的启发做了进一步探究:如图2,在△ABC外分别以AB,AC为斜边作Rt△AEB与Rt△AFC,并使∠FAC=∠EAB=30°,取BC的中点D,连接DE,EF后发现,两者间存在一定的数量关系且夹角度数一定,请你帮助小明求出 的值及∠DEF的度数.
(3)、小颖受到启发也做了探究:如图3,在△ABC外分别以AB,AC为底边作等腰三角形AEB和等腰三角形AFC,并使∠CAF+∠EAB=90°,取BC的中点D,连接DE,EF后发现,当给定∠EAB=α时,两者间也存在一定的数量关系且夹角度数一定,若AE=m,AB=n,请你帮助小颖用含m,n的代数式直接写出 的值,并用含α的代数式直接表示∠DEF的度数.
26. 如图,在平面直角坐标系中,抛物线y=﹣ x2+bx+c与x轴交于B,C两点,与y轴交于点A,直线y=﹣ x+2经过A,C两点,抛物线的对称轴与x轴交于点D,直线MN与对称轴交于点G,与抛物线交于M,N两点(点N在对称轴右侧),且MN∥x轴,MN=7.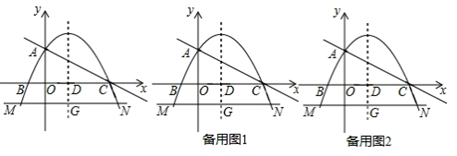 (1)、求此抛物线的解析式.(2)、求点N的坐标.(3)、过点A的直线与抛物线交于点F,当tan∠FAC= 时,求点F的坐标.(4)、过点D作直线AC的垂线,交AC于点H,交y轴于点K,连接CN,△AHK沿射线AC以每秒1个单位长度的速度移动,移动过程中△AHK与四边形DGNC产生重叠,设重叠面积为S,移动时间为t(0≤t≤ ),请直接写出S与t的函数关系式.
(1)、求此抛物线的解析式.(2)、求点N的坐标.(3)、过点A的直线与抛物线交于点F,当tan∠FAC= 时,求点F的坐标.(4)、过点D作直线AC的垂线,交AC于点H,交y轴于点K,连接CN,△AHK沿射线AC以每秒1个单位长度的速度移动,移动过程中△AHK与四边形DGNC产生重叠,设重叠面积为S,移动时间为t(0≤t≤ ),请直接写出S与t的函数关系式.