甘肃省2019年中考数学试卷
试卷更新日期:2019-11-04 类型:中考真卷
一、单选题
-
1. 下列四个图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在0,2,﹣3,﹣ 这四个数中,最小的数是( )A、0 B、2 C、﹣3 D、﹣3. 使得式子 有意义的x的取值范围是( )A、x≥4 B、x>4 C、x≤4 D、x<44. 计算(﹣2a)2•a4的结果是( )A、﹣4a6 B、4a6 C、﹣2a6 D、﹣4a85. 如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=48°,那么∠2的度数是( )
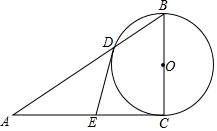
2. 在0,2,﹣3,﹣ 这四个数中,最小的数是( )A、0 B、2 C、﹣3 D、﹣3. 使得式子 有意义的x的取值范围是( )A、x≥4 B、x>4 C、x≤4 D、x<44. 计算(﹣2a)2•a4的结果是( )A、﹣4a6 B、4a6 C、﹣2a6 D、﹣4a85. 如图,将一块含有30°的直角三角板的顶点放在直尺的一边上,若∠1=48°,那么∠2的度数是( ) A、48° B、78° C、92° D、102°6. 已知点 在 轴上,则点 的坐标是( )A、 B、 C、 D、7. 若一元二次方程x2﹣2kx+k2=0的一根为x=﹣1,则k的值为( )A、﹣1 B、0 C、1或﹣1 D、2或08. 如图,AB是⊙O的直径,点C,D是圆上两点,且∠AOC=126°,则∠CDB=( )
A、48° B、78° C、92° D、102°6. 已知点 在 轴上,则点 的坐标是( )A、 B、 C、 D、7. 若一元二次方程x2﹣2kx+k2=0的一根为x=﹣1,则k的值为( )A、﹣1 B、0 C、1或﹣1 D、2或08. 如图,AB是⊙O的直径,点C,D是圆上两点,且∠AOC=126°,则∠CDB=( )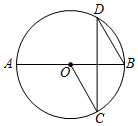 A、54° B、64° C、27° D、37°9. 甲,乙两个班参加了学校组织的2019年“国学小名士”国学知识竞赛选拔赛,他们成绩的平均数、中位数、方差如下表所示,规定成绩大于等于95分为优异,则下列说法正确的是( )
A、54° B、64° C、27° D、37°9. 甲,乙两个班参加了学校组织的2019年“国学小名士”国学知识竞赛选拔赛,他们成绩的平均数、中位数、方差如下表所示,规定成绩大于等于95分为优异,则下列说法正确的是( )参加人数
平均数
中位数
方差
甲
45
94
93
5.3
乙
45
94
95
4.8
A、甲、乙两班的平均水平相同 B、甲、乙两班竞赛成绩的众数相同 C、甲班的成绩比乙班的成绩稳定 D、甲班成绩优异的人数比乙班多10. 如图是二次函数y=ax2+bx+c的图象,对于下列说法:①ac>0,②2a+b>0,③4ac<b2 , ④a+b+c<0,⑤当x>0时,y随x的增大而减小,其中正确的是( )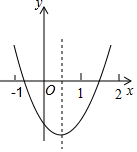 A、①②③ B、①②④ C、②③④ D、③④⑤
A、①②③ B、①②④ C、②③④ D、③④⑤二、填空题
-
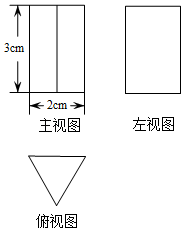
11. 分解因式:x3y﹣4xy= .12. 不等式组 的最小整数解是.13. 分式方程 的解为.14. 在△ABC中∠C=90°,tanA= ,则cosB=.15. 已知某几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的左视图的面积为.
 16. 如图,在Rt△ABC中,∠C=90°,AC=BC=2,点D是AB的中点,以A、B为圆心,AD、BD长为半径画弧,分别交AC、BC于点E、F,则图中阴影部分的面积为.
16. 如图,在Rt△ABC中,∠C=90°,AC=BC=2,点D是AB的中点,以A、B为圆心,AD、BD长为半径画弧,分别交AC、BC于点E、F,则图中阴影部分的面积为.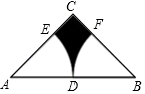 17. 如图,在矩形ABCD中,AB=10,AD=6,E为BC上一点,把△CDE沿DE折叠,使点C落在AB边上的F处,则CE的长为 .
17. 如图,在矩形ABCD中,AB=10,AD=6,E为BC上一点,把△CDE沿DE折叠,使点C落在AB边上的F处,则CE的长为 .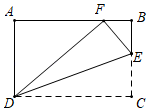 18. 如图,每一图中有若干个大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,如果第n幅图中有2019个菱形,则n=.
18. 如图,每一图中有若干个大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,如果第n幅图中有2019个菱形,则n=.
三、解答题
-
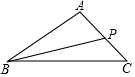
19. 计算:(﹣ )﹣2+(2019﹣π)0﹣ tan60°﹣|﹣3|.20. 如图,在△ABC中,点P是AC上一点,连接BP,求作一点M,使得点M到AB和AC两边的距离相等,并且到点B和点P的距离相等.(不写作法,保留作图痕迹)
 21. 中国古代入民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题,原文:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?22. 为了保证人们上下楼的安全,楼梯踏步的宽度和高度都要加以限制.中小学楼梯宽度的范围是260mm~300mm含(300mm),高度的范围是120mm~150mm(含150mm).如图是某中学的楼梯扶手的截面示意图,测量结果如下:AB,CD分别垂直平分踏步EF,GH,各踏步互相平行,AB=CD,AC=900mm,∠ACD=65°,试问该中学楼梯踏步的宽度和高度是否符合规定.(结果精确到1mm,参考数据:sin65°≈0.906,cos65°≈0.423)
21. 中国古代入民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题,原文:今有三人共车,二车空;二人共车,九人步,问人与车各几何?译文为:今有若干人乘车,每3人共乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问共有多少人,多少辆车?22. 为了保证人们上下楼的安全,楼梯踏步的宽度和高度都要加以限制.中小学楼梯宽度的范围是260mm~300mm含(300mm),高度的范围是120mm~150mm(含150mm).如图是某中学的楼梯扶手的截面示意图,测量结果如下:AB,CD分别垂直平分踏步EF,GH,各踏步互相平行,AB=CD,AC=900mm,∠ACD=65°,试问该中学楼梯踏步的宽度和高度是否符合规定.(结果精确到1mm,参考数据:sin65°≈0.906,cos65°≈0.423)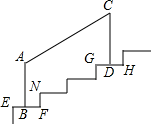 23. 在甲乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1,2,3,4,乙口袋中的小球上分别标有数字2,3,4,先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中摸出一个小球,记下数字为n.(1)、请用列表或画树状图的方法表示出所有(m,n)可能的结果;(2)、若m,n都是方程x2﹣5x+6=0的解时,则小明获胜;若m,n都不是方程x2﹣5x+6=0的解时,则小利获胜,问他们两人谁获胜的概率大?24. 良好的饮食对学生的身体、智力发育和健康起到了极其重要的作用,荤菜中蛋白质、钙、磷及脂溶性维生素优于素食,而素食中不饱和脂肪酸、维生素和纤维素又优于荤食,只有荤食与素食适当搭配,才能强化初中生的身体素质.某校为了了解学生的体质健康状况,以便食堂为学生提供合理膳食,对本校七年级、八年级学生的体质健康状况进行了调查,过程如下:
23. 在甲乙两个不透明的口袋中,分别有大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字1,2,3,4,乙口袋中的小球上分别标有数字2,3,4,先从甲袋中任意摸出一个小球,记下数字为m,再从乙袋中摸出一个小球,记下数字为n.(1)、请用列表或画树状图的方法表示出所有(m,n)可能的结果;(2)、若m,n都是方程x2﹣5x+6=0的解时,则小明获胜;若m,n都不是方程x2﹣5x+6=0的解时,则小利获胜,问他们两人谁获胜的概率大?24. 良好的饮食对学生的身体、智力发育和健康起到了极其重要的作用,荤菜中蛋白质、钙、磷及脂溶性维生素优于素食,而素食中不饱和脂肪酸、维生素和纤维素又优于荤食,只有荤食与素食适当搭配,才能强化初中生的身体素质.某校为了了解学生的体质健康状况,以便食堂为学生提供合理膳食,对本校七年级、八年级学生的体质健康状况进行了调查,过程如下:收集数据:从七、八年级两个年级中各抽取15名学生,进行了体质健康测试,测试成绩(百分制)如下:
七年级:748175767075757981707480916982
八年级:819483778380817081737882807050
整理数据:
年级
x<60
60≤x<80
80≤x<90
90≤x≤100
七年级
0
10
4
1
八年级
1
5
8
1
(说明:90分及以上为优秀,80~90分(不含90分)为良好,60~80分(不含80分)为及格,60分以下为不及格)
分析数据:
年级
平均数
中位数
众数
七年级
75
75
八年级
77.5
80
得出结论:
(1)、根据上述数据,将表格补充完整;(2)、可以推断出几年级学生的体质健康状况更好一些,并说明理由;(3)、若七年级共有300名学生,请估计七年级体质健康成绩优秀的学生人数.25. 如图,一次函数 的图象与反比例函数 的图象相交于 两点,与 轴相交于点 .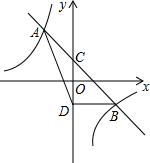 (1)、求一次函数与反比例函数的解析式;(2)、若点 与点 关于 轴对称,求 的面积;(3)、若 是反比例函数 上的两点,当 时,比 与 的大小关系.26. 如图,在正方形 中,点 是 的中点,连接 ,过点 作 交 于点 ,交 于点 .
(1)、求一次函数与反比例函数的解析式;(2)、若点 与点 关于 轴对称,求 的面积;(3)、若 是反比例函数 上的两点,当 时,比 与 的大小关系.26. 如图,在正方形 中,点 是 的中点,连接 ,过点 作 交 于点 ,交 于点 .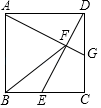 (1)、证明: ;(2)、连接 ,证明: .
(1)、证明: ;(2)、连接 ,证明: .