浙江省湖州四中2020届九年级上学期数学第一次月考试卷

试卷更新日期：2019-11-04 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分.）

1. 下列说法正确的是（）

A、任意抛掷一枚质地均匀的硬币10次，则“有5次正面朝上”是必然事件 B、明天的降水概率为40%，则“明天下雨”是确定事件 C、篮球队员在罚球线上投篮一次，则“投中”是随机事件 D、a是实数，则“|a|≥0”是不可能事件

查看试题解析
2. 对于二次函数 $y = - {(x - 1)}^{2} + 2$ 的图象与性质，下列说法正确的是（）

A、对称轴是直线 $x = 1$ ，最小值是 $2$ B、对称轴是直线 $x = 1$ ，最大值是 $2$ C、对称轴是直线 $x = - 1$ ，最小值是 $2$ D、对称轴是直线 $x = - 1$ ，最大值是 $2$

查看试题解析
3. 下列二次函数的图象通过平移能与二次函数y=x²-2x-1的图象重合的是（）

A、y=2x²-x+1 B、y=x²+2x+1 C、y= $\frac{1}{2}$ x²-2x-1 D、y= $\frac{1}{2}$ x²+2x+1

查看试题解析
4. 已知点A(1，y₁)，B(2，y₂)在抛物线y=−(x+1)²+2上,则下列结论正确的是（）

A、 $2 \leq y_{1} < y_{2}$ B、 $2 \leq y_{2} < y_{1}$ C、 $y_{1} < y_{2} < 2$ D、 $y_{2} < y_{1} < 2$

查看试题解析
5. 笔筒中有9支型号、颜色完全相同的铅笔，将它们逐一标上1-9的号码，若从笔筒中任意抽出一支铅笔，则抽到编号是3的倍数的概率是（）

A、 $\frac{1}{9}$ B、 $\frac{2}{9}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
6. 已知A（x₁ ， y₁），B（x₂ ， y₂）是二次函数上y=ax²-2ax+a-c（a≠0）的两点，若x₁≠x₂ ，且y₁=y₂ ，则当自变量x的值取x₁+x₂时，函数值为（）

A、-c B、c C、-a+c D、a-c

查看试题解析
7. 在同一平面直角坐标系中，若抛物线y=x²+（2m-1）x+2m-4与y=x²-（3m+n）x+n关于y轴对称，则符合条件的m ， n的值为（）

A、 $m = \frac{5}{7}$ ， n=- $\frac{18}{7}$ B、m=5，n=-6 C、m=-1，n=6 D、m=1，n=-2

查看试题解析
8. 如图是王阿姨晚饭后步行的路程s（单位：m）与时间t（单位：min）的函数图象，其中曲线段AB是以B为顶点的抛物线一部分．下列说法不正确的是（）

A、25min～50min，王阿姨步行的路程为800m B、线段CD的函数解析式为s=32t+400（25≤t≤50） C、5min～20min，王阿姨步行速度由慢到快 D、曲线段AB的函数解析式为s=-3（t-20）2+1200（5≤t≤20）

查看试题解析
9. 如图，二次函数y=ax²+bx+c（a $\neq$ 0）的图象过点（-2，0），对称轴为直线x=1.有以下结论：
①abc>0；②8a+c>0；③若A（x₁ ， m），B（x₂ ， m）是抛物线上的两点，当x=x₁+x₂时，y=c；④若方程a（x+2）（4-x）=-2的两根为x₁ ， x₂ ，且x₁<x₂ ，则-2 $\leq$ x₁<x₂<4.其中结论正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，直线 $y = k x + b$ (k、b为常数)分别与x轴、y轴交于点A(−4，0)、B(0，3)，抛物线 $y = - x^{2} + 4 x + 1$ 与y轴交于点C，点E在抛物线 $y = - x^{2} + 4 x + 1$ 的对称轴上移动，点F在直线AB上移动，CE+EF的最小值是（）

A、2 B、4 C、2.5 D、3

查看试题解析

二、填空题（本大题共6个小题，每小题3分，共18分）

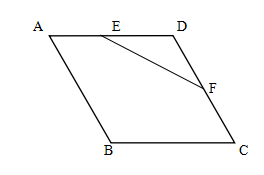
11. 函数 $y=$ $（ x+1 ）^{2}$ $+9$ 图像的顶点坐标是

查看试题解析
12. 在一个不透明的盒子中装有a个除颜色外完全相同的球,其中只有6个白球。若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子。通过大量重复试验后,发现摸到白球的频率稳定在20%左右,则a的值约为

查看试题解析
13. 已知 $y = - \frac{1}{4} x^{2} - 3 x + 4$ （-10≤x≤0），则函数y的取值范围是

查看试题解析
14. 函数 $y = {\begin{cases} x^{2} + 1 （ x \leq 2 ） \\ 2 x （ x > 2 ） \end{cases}$ ,则当函数值y=8时,自变量x的值是

查看试题解析
15. 如图，菱形ABCD的边长为8，∠BAD=60°，点E是AD上一动点（不与A、D重合），点F是CD上一动点，且AE+CF=8，则△DEF面积的最大值为.

查看试题解析
16. 阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”。例如，点M(1，3)的特征线有：x=1，y=3，y=x+2，y=−x+4.如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线 $y = \frac{1}{4} {(x - a)}^{2} + b$ 经过B. C两点，顶点D在正方形内部。

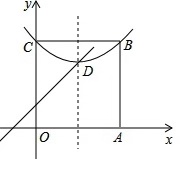(1)、写出点M（2，3）任意两条特征线

(2)、若点D有一条特征线是y=x+1，求此抛物线的解析式

查看试题解析

三、解答题（本题共9小题，共72分）

17. 将抛物线 $y_{1} {=2x}^{2}$ 先向下平移2个单位，再向右平移3个单位得到抛物线 $y_{2}$

(1)、直接写出平移后的抛物线 $y_{2}$ 的解析式；

(2)、求出 $y_{2}$ 与x轴的交点坐标；

(3)、当 $y_{2}$ ＜0时，写出 $x$ 的取值范围.

查看试题解析
18. 已知：如图，二次函数y=ax²+bx+c的图象与x轴交于A、B两点，其中A点坐标为(−1，0)，B点坐标为(5，0)点C(0，5)，M为它的顶点。

(1)、求抛物线的解析式；

(2)、求△MCB的面积。

查看试题解析
19. 杨老师为了了解所教班级学生课后复习的具体情况，对本班部分学生进行了一个月的跟踪调查，然后将调查结果分成四类：A：优秀；B：良好；C：一般；D：较差。并将调查结果绘制成以下两幅不完整的统计图．
请根据统计图解答下列问题：

(1)、本次调查中，杨老师一共调查了名学生，其中C类女生有名，D类男生有名；

(2)、补全上面的条形统计图和扇形统计图；

(3)、在此次调查中，小明、小芳属于D类。为了进步，他们请杨老师从被调查的A类学生中随机选取两位同学，和他们进行“一帮一”的课后互助学习。请结合树状图或者列表，求出所选的同学恰好有一位女同学的概率．

查看试题解析
20. 如图，二次函数 ${y=(x+2)}^{2} +m$ 的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y=kx+b的图象经过该二次函数图象上的点A(−1，0)及点B.

(1)、求二次函数与一次函数的解析式；

(2)、根据图象，写出满足 ${(x+2)}^{2} +m \geq kx+b$ 的x的取值范围。

查看试题解析
21. 已知，抛物线y=-x²+bx+c经过点A（-1，0）和C（0，3）.

(1)、求抛物线的解析式；

(2)、设点M在抛物线的对称轴上，当△MAC是以AC为直角边的直角三角形时，求点M的坐标.

查看试题解析
22. 2018年非洲猪瘟疫情爆发后，专家预测，2019年我市猪肉售价将逐月上涨，每千克猪肉的售价 $y_{1}$ （元）与月份x（1≤x≤12，且x为整数）之间满足一次函数，如下表所示。每千克猪肉的成本 $y_{2}$ （元）与月份x（1≤x≤12，且x为整数）之间满足二次函数关系，且3月份每千克猪肉的成本全年最低，为9元，如图所示

月份x

…

3

4

5

6

…

售价y₁/元

…

12

14

16

18

…

(1)、求 $y_{1}$ 与x之间的函数关系式

(2)、求 $y_{2}$ 与x之间的函数关系式

(3)、设销售每千克猪肉所获得的利润为w（元），求w与x之间的函数关系式，哪个月份销售每千克猪肉所获得的利润最大？最大利润是多少元？

查看试题解析
23. 阅读下列材料，解决材料后的问题：
材料一：对于实数x、y，我们将x与y的“友好数”用f（x，y）表示，定义为： $f (x ， y) = \frac{x}{y + 2}$ ，例如17与16的友好数为 $f (17 ， 16) = \frac{17}{16 + 2} = \frac{17}{18}$ .

材料二：对于实数 $x$ ，用 $[x]$ 表示不超过实数 $x$ 的最大整数，即满足条件 $[x]$ ≤ $x$ ＜ $[x] + 1$ ，例如：

$[- 1.5] = [- 1.6] = - 2$ ， $[0] = [0.7] = 0$ ， $[2.2] = [2.7] = 2$ ，……

(1)、由材料一知： $x^{2} + 2$ 与1的“友好数”可以用 $f (x^{2} + 2 ， 1)$ 表示，已知 $f (x^{2} + 2 ， 1) = 2$ ，请求出 $x$ 的值；

(2)、已知 $[\frac{1}{2} a - 1] = - 3$ ，请求出实数a的取值范围；

(3)、已知实数 $x 、 m$ 满足条件 $x - 2 [x] = \frac{7}{2}$ ，且 $m \geq 2x + \frac{11}{2}$ ，请求 $f (x ， m^{2} - \frac{3}{2} m)$ 的最小值.

查看试题解析
24. 如图(1)，在平面直角坐标系x Oy中，直线y=2x+4与y轴交于点A，与x轴交于点B，抛物线C₁：y=− $\frac{1}{4}$ x²+bx+c过A，B两点，与x轴的另一交点为点C.

(1)、求抛物线C₁的解析式及点C的坐标；

(2)、如图(2)，作抛物线C₂ ，使得抛物线C₂与C₁恰好关于原点对称，C₂与C₁在第一象限内交于点D，连接AD，CD，请直接写出抛物线C2的解析式和点D的坐标

(3)、已知抛物线C₂的顶点为M，设P为抛物线C₁对称轴上一点，Q为直线y=2x+4上一点，是否存在以点M，Q，P，B为顶点的四边形为平行四边形?若存在，直接写出点P的坐标；若不存在，请说明理由

查看试题解析

月份x	…	3	4	5	6	…
售价y₁/元	…	12	14	16	18	…