2017年湖南省张家界市中考数学试卷
试卷更新日期:2017-07-13 类型:中考真卷
一、选择题
-
1. ﹣2017的相反数是( )A、﹣2017 B、2017 C、﹣ D、2. 正在修建的黔张常铁路,横跨渝、鄂、湘三省,起于重庆市黔江区黔江站,止于常德市武陵区常德站.铁路规划线路总长340公里,工程估算金额37500000000元.将数据37500000000用科学记数法表示为( )
A、0.375×1011 B、3.75×1011 C、3.75×1010 D、375×1083. 如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=30°,则∠BOC的度数是( )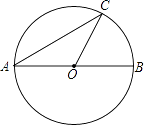 A、30° B、45° C、55° D、60°4. 下列运算正确的有( )A、5ab﹣ab=4 B、(a2)3=a6 C、(a﹣b)2=a2﹣b2 D、=±35. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )
A、30° B、45° C、55° D、60°4. 下列运算正确的有( )A、5ab﹣ab=4 B、(a2)3=a6 C、(a﹣b)2=a2﹣b2 D、=±35. 如图,D,E分别是△ABC的边AB,AC上的中点,如果△ADE的周长是6,则△ABC的周长是( )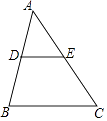 A、6 B、12 C、18 D、246.
A、6 B、12 C、18 D、246.如图是一个正方体的表面展开图,则原正方体中与“美”字所在面相对的面上标的字是( )
 A、丽 B、张 C、家 D、界7. 某校高一年级今年计划招四个班的新生,并采取随机摇号的方法分班,小明和小红既是该校的高一新生,又是好朋友,那么小明和小红分在同一个班的机会是( )A、 B、 C、 D、8. 在同一平面直角坐标系中,函数y=mx+m(m≠0)与y= (m≠0)的图象可能是( )A、
A、丽 B、张 C、家 D、界7. 某校高一年级今年计划招四个班的新生,并采取随机摇号的方法分班,小明和小红既是该校的高一新生,又是好朋友,那么小明和小红分在同一个班的机会是( )A、 B、 C、 D、8. 在同一平面直角坐标系中,函数y=mx+m(m≠0)与y= (m≠0)的图象可能是( )A、 B、
B、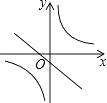 C、
C、 D、
D、
二、填空题
-
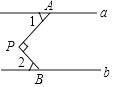
9. 不等式组 的解集是 .10. 因式分解:x3﹣x= .11. 如图,a∥b,PA⊥PB,∠1=35°,则∠2的度数是 .
 12. 已知一元二次方程x2﹣3x﹣4=0的两根是m,n,则m2+n2= .13. 某校组织学生参加植树活动,活动结束后,统计了九年级甲班50名学生每人植树的情况,绘制了如下的统计表:
12. 已知一元二次方程x2﹣3x﹣4=0的两根是m,n,则m2+n2= .13. 某校组织学生参加植树活动,活动结束后,统计了九年级甲班50名学生每人植树的情况,绘制了如下的统计表:植树棵数
3
4
5
6
人数
20
15
10
5
那么这50名学生平均每人植树棵.
14. 如图,在正方形ABCD中,AD=2 ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 .
三、解答题
-
15. 计算:( )﹣1+2cos30°﹣| ﹣1|+(﹣1)2017 .16. 先化简(1﹣ )÷ ,再从不等式2x﹣1<6的正整数解中选一个适当的数代入求值.17. 如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
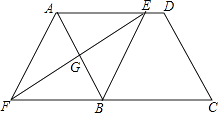 (1)、求证:△AGE≌△BGF;(2)、试判断四边形AFBE的形状,并说明理由.18. 某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共140件,进行手绘设计后了出售,所获利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如下表:
(1)、求证:△AGE≌△BGF;(2)、试判断四边形AFBE的形状,并说明理由.18. 某校组织“大手拉小手,义卖献爱心”活动,购买了黑白两种颜色的文化衫共140件,进行手绘设计后了出售,所获利润全部捐给山区困难孩子.每件文化衫的批发价和零售价如下表:批发价(元)
零售价(元)
黑色文化衫
10
25
白色文化衫
8
20
假设文化衫全部售出,共获利1860元,求黑白两种文化衫各多少件?
19. 位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824) 20. 阅读理解题:
20. 阅读理解题:定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加、减,乘法运算与整式的加、减、乘法运算类似.
例如计算:(2﹣i)+(5+3i)=(2+5)+(﹣1+3)i=7+2i;
(1+i)×(2﹣i)=1×2﹣i+2×i﹣i2=2+(﹣1+2)i+1=3+i;
根据以上信息,完成下列问题:
(1)、填空:i3= , i4=;(2)、计算:(1+i)×(3﹣4i);(3)、计算:i+i2+i3+…+i2017 .21. 在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.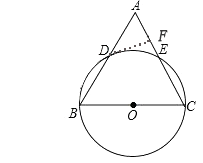 (1)、求证:DF是⊙O的切线;(2)、分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.
(1)、求证:DF是⊙O的切线;(2)、分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.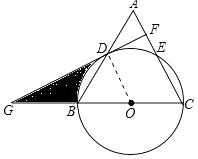 22. 为了丰富同学们的课余生活,某学校计划举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生必须从“A(洪家关),B(天门山),C(大峡谷),D(黄龙洞)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
22. 为了丰富同学们的课余生活,某学校计划举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生必须从“A(洪家关),B(天门山),C(大峡谷),D(黄龙洞)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图.
请你根据图中所提供的信息,完成下列问题:
(1)、本次调查的学生人数为;(2)、在扇形统计图中,“天门山”部分所占圆心角的度数为;(3)、请将两个统计图补充完整;(4)、若该校共有2000名学生,估计该校最想去大峡谷的学生人数为 .23.已知抛物线c1的顶点为A(﹣1,4),与y轴的交点为D(0,3).
 (1)、求c1的解析式;(2)、若直线l1:y=x+m与c1仅有唯一的交点,求m的值;(3)、若抛物线c1关于y轴对称的抛物线记作c2 , 平行于x轴的直线记作l2:y=n.试结合图形回答:当n为何值时,l2与c1和c2共有:①两个交点;②三个交点;③四个交点;(4)、若c2与x轴正半轴交点记作B,试在x轴上求点P,使△PAB为等腰三角形.
(1)、求c1的解析式;(2)、若直线l1:y=x+m与c1仅有唯一的交点,求m的值;(3)、若抛物线c1关于y轴对称的抛物线记作c2 , 平行于x轴的直线记作l2:y=n.试结合图形回答:当n为何值时,l2与c1和c2共有:①两个交点;②三个交点;③四个交点;(4)、若c2与x轴正半轴交点记作B,试在x轴上求点P,使△PAB为等腰三角形.