2017年四川省内江市中考数学试卷

试卷更新日期：2017-07-13 类型：中考真卷

进入出卷网下载

一、选择题

1. 下面四个数中比﹣5小的数是（）

A、1 B、0 C、﹣4 D、﹣6

查看试题解析
2. PM2.5是指大气中直径小于或等于2.5μm（1μm=0.000001m）的颗粒物，也称为可入肺颗粒物，它们还有一定量的有毒、有害物质，对人体健康和大气环境质量有很大影响.2.3μm用科学记数法可表示为（）

A、23×10^﹣5m B、2.3×10^﹣5m C、2.3×10^﹣6m D、0.23×10^﹣7m

查看试题解析
3. 为了解某市老人的身体健康状况，需要抽取部分老人进行调查，下列抽取老人的方法最合适的是（）

A、随机抽取100位女性老人 B、随机抽取100位男性老人 C、随机抽取公园内100位老人 D、在城市和乡镇各选10个点，每个点任选5位老人

查看试题解析
4. 如图，直线m∥n，直角三角板ABC的顶点A在直线m上，则∠α的余角等于（）

A、19° B、38° C、42° D、52°

查看试题解析
5. 由一些大小相同的小正方体搭成的几何体的俯视图如图所示，其中正方形中的数字表示该位置上的小正方体的个数，那么该几何体的主视图是（）

A、 B、 C、 D、

查看试题解析
6. 下列图形：平行四边形、矩形、菱形、圆、等腰三角形，这些图形中只是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 某中学对该校九年级45名女学生进行了一次立定跳远测试，成绩如表：
跳远成绩
160
170
180
190
200
210
人数
3
9
6
9
15
3
这些立定跳远成绩的中位数和众数分别是（）

A、9，9 B、15，9 C、190，200 D、185，200

查看试题解析
8. 下列计算正确的是（）

A、3x²y+5xy=8x³y² B、（x+y）²=x²+y² C、（﹣2x）²÷x=4x D、 $\frac{y}{x - y}$ + $\frac{x}{y - x}$ =1

查看试题解析
9. 端午节前夕，某超市用1680元购进A、B两种商品共60件，其中A型商品每件24元，B型商品每件36元．设购买A型商品x件、B型商品y件，依题意列方程组正确的是（）

A、 ${\begin{matrix} x + y = 60 \\ 36 x + 24 y = 1680 \end{matrix}$ B、 ${\begin{matrix} x + y = 60 \\ 24 x + 36 y = 1680 \end{matrix}$ C、 ${\begin{matrix} 36 x + 24 y = 60 \\ x + y = 1680 \end{matrix}$ D、 ${\begin{matrix} 24 x + 36 y = 60 \\ x + y = 1680 \end{matrix}$

查看试题解析
10. 不等式组 ${\begin{matrix} 3 x + 7 \geq 2 \\ 2 x - 9 < 1 \end{matrix}$ 的非负整数解的个数是（）

A、4 B、5 C、6 D、7

查看试题解析
11. 如图，在矩形AOBC中，O为坐标原点，OA、OB分别在x轴、y轴上，点B的坐标为（0，3 $\sqrt{3}$ ），∠ABO=30°，将△ABC沿AB所在直线对折后，点C落在点D处，则点D的坐标为（）

A、（ $\frac{3}{2}$ ， $\frac{3}{2} \sqrt{3}$ ） B、（2， $\frac{3}{2} \sqrt{3}$ ） C、（ $\frac{3}{2} \sqrt{3}$ ， $\frac{3}{2}$ ） D、（ $\frac{3}{2}$ ，3﹣ $\frac{3}{2} \sqrt{3}$ ）

查看试题解析
12.
如图，过点A₀（2，0）作直线l：y= $\frac{\sqrt{3}}{3}$ x的垂线，垂足为点A₁ ，过点A₁作A₁A₂⊥x轴，垂足为点A₂ ，过点A₂作A₂A₃⊥l，垂足为点A₃ ， …，这样依次下去，得到一组线段：A₀A₁ ， A₁A₂ ， A₂A₃ ， …，则线段A₂₀₁₆A₂₁₀₇的长为（）

A、（ $\frac{\sqrt{3}}{2}$ ）²⁰¹⁵ B、（ $\frac{\sqrt{3}}{2}$ ）²⁰¹⁶ C、（ $\frac{\sqrt{3}}{2}$ ）²⁰¹⁷ D、（ $\frac{\sqrt{3}}{2}$ ）²⁰¹⁸

查看试题解析

二、填空题

13. 分解因式：3x²﹣18x+27= ．

查看试题解析
14. 在函数y= $\frac{1}{x - 3}$ + $\sqrt{x - 2}$ 中，自变量x的取值范围是．

查看试题解析
15. 如图，AB是⊙O的直径，弦CD⊥AB于点E，⊙O的半径为 $\sqrt{3}$ ，弦CD的长为3cm，则图中阴影部分面积是．．

查看试题解析
16. 如图，正方形ABCD中，BC=2，点M是边AB的中点，连接DM，DM与AC交于点P，点E在DC上，点F在DP上，且∠DFE=45°．若PF= $\frac{\sqrt{5}}{6}$ ，则CE= ．

查看试题解析

三、解答题

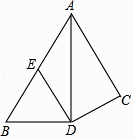
17. 计算：﹣1²⁰¹⁷﹣丨1﹣ $\frac{\sqrt{3}}{3} t a n 60 °$ 丨+ $\sqrt{{(- 2)}^{2}}$ ×（ $\frac{1}{2}$ ）^﹣2+（2017﹣π）⁰ ．

查看试题解析
18. 如图，AD平分∠BAC，AD⊥BD，垂足为点D，DE∥AC．
求证：△BDE是等腰三角形．

查看试题解析
19. 小明随机调查了若干市民租用共享单车的骑车时间t（单位：分），将获得的数据分成四组，绘制了如下统计图（A：0＜t≤10，B：10＜t≤20，C：20＜t≤30，D：t＞30），根据图中信息，解答下列问题：

(1)、这项被调查的总人数是多少人？

(2)、试求表示A组的扇形统计图的圆心角的度数，补全条形统计图；

(3)、如果小明想从D组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况，请用列表或画树状图的方法求出恰好选中甲的概率．

查看试题解析
20.
如图，某人为了测量小山顶上的塔ED的高，他在山下的点A处测得塔尖点D的仰角为45°，再沿AC方向前进60m到达山脚点B，测得塔尖点D的仰角为60°，塔底点E的仰角为30°，求塔ED的高度．（结果保留根号）

查看试题解析
21. 已知A（﹣4，2）、B（n，﹣4）两点是一次函数y=kx+b和反比例函数y= $\frac{m}{x}$ 图象的两个交点．

(1)、求一次函数和反比例函数的解析式；

(2)、求△AOB的面积；

(3)、观察图象，直接写出不等式kx+b﹣ $\frac{m}{x}$ ＞0的解集．

查看试题解析

四、填空题

22. 若实数x满足x²﹣2x﹣1=0，则2x³﹣7x²+4x﹣2017= ．

查看试题解析
23. 如图，四边形ABCD中，AD∥BC，CM是∠BCD的平分线，且CM⊥AB，M为垂足，AM= $\frac{1}{3}$ AB．若四边形ABCD的面积为 $\frac{15}{7}$ ，则四边形AMCD的面积是．

查看试题解析
24. 设α、β是方程（x+1）（x﹣4）=﹣5的两实数根，则 $\frac{β^{3}}{α} + \frac{α^{3}}{β}$ = ．

查看试题解析
25.
如图，已知直线l₁∥l₂ ， l₁、l₂之间的距离为8，点P到直线l₁的距离为6，点Q到直线l₂的距离为4，PQ=4 $\sqrt{30}$ ，在直线l₁上有一动点A，直线l₂上有一动点B，满足AB⊥l₂ ，且PA+AB+BQ最小，此时PA+BQ= ．

查看试题解析

五、解答题

26. 观察下列等式：
第一个等式： $a_{1} = \frac{2}{1 + 3 \times 2 + 2 \times 2^{2}} = \frac{1}{2 + 1} - \frac{1}{2^{2} + 1}$
第二个等式： $a_{2} = \frac{2^{2}}{1 + 3 \times 2^{2} + 2 \times {(2^{2})}^{2}} = \frac{1}{2^{2} + 1} - \frac{1}{2^{3} + 1}$
第三个等式： $a_{3} = \frac{2^{3}}{1 + 3 \times 2^{3} + 2 \times {(2^{3})}^{2}} = \frac{1}{2^{3} + 1} - \frac{1}{2^{4} + 1}$
第四个等式： $a_{4} = \frac{2^{4}}{1 + 3 \times 2^{4} + 2 \times {(2^{4})}^{2}} = \frac{1}{2^{4} + 1} - \frac{1}{2^{5} + 1}$
按上述规律，回答下列问题：

(1)、请写出第六个等式：a₆==；

(2)、用含n的代数式表示第n个等式：a_n==；

(3)、a₁+a₂+a₃+a₄+a₅+a₆=（得出最简结果）；

(4)、计算：a₁+a₂+…+a_n ．

查看试题解析
27. 如图，在⊙O中，直径CD垂直于不过圆心O的弦AB，垂足为点N，连接AC，点E在AB上，且AE=CE

(1)、求证：AC²=AE•AB；

(2)、过点B作⊙O的切线交EC的延长线于点P，试判断PB与PE是否相等，并说明理由；

(3)、设⊙O半径为4，点N为OC中点，点Q在⊙O上，求线段PQ的最小值．

查看试题解析
28.
如图，在平面直角坐标系中，抛物线y=ax²+bx+c（a≠0）与y轴交与点C（0，3），与x轴交于A、B两点，点B坐标为（4，0），抛物线的对称轴方程为x=1．

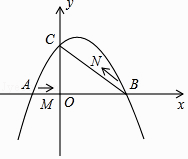(1)、求抛物线的解析式；

(2)、点M从A点出发，在线段AB上以每秒3个单位长度的速度向B点运动，同时点N从B点出发，在线段BC上以每秒1个单位长度的速度向C点运动，其中一个点到达终点时，另一个点也停止运动，设△MBN的面积为S，点M运动时间为t，试求S与t的函数关系，并求S的最大值；

(3)、在点M运动过程中，是否存在某一时刻t，使△MBN为直角三角形？若存在，求出t值；若不存在，请说明理由．

查看试题解析

跳远成绩	160	170	180	190	200	210
人数	3	9	6	9	15	3