2017年辽宁省大连市中考数学试卷
试卷更新日期:2017-07-13 类型:中考真卷
一、选择题
-
1. 在实数﹣1,0,3, 中,最大的数是( )A、﹣1 B、0 C、3 D、2. 一个几何体的三视图如图所示,则这个几何体是( )
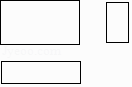 A、圆锥 B、长方体 C、圆柱 D、球3. 计算 ﹣ 的结果是( )A、 B、 C、 D、4. 计算(﹣2a3)2的结果是( )A、﹣4a5 B、4a5 C、﹣4a6 D、4a65. 如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( )
A、圆锥 B、长方体 C、圆柱 D、球3. 计算 ﹣ 的结果是( )A、 B、 C、 D、4. 计算(﹣2a3)2的结果是( )A、﹣4a5 B、4a5 C、﹣4a6 D、4a65. 如图,直线a,b被直线c所截,若直线a∥b,∠1=108°,则∠2的度数为( ) A、108° B、82° C、72° D、62°6. 同时抛掷两枚质地均匀的硬币,两枚硬币全部正面向上的概率为( )A、 B、 C、 D、7. 在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(﹣1,﹣1),B(1,2),平移线段AB,得到线段A′B′,已知A′的坐标为(3,﹣1),则点B′的坐标为( )A、(4,2) B、(5,2) C、(6,2) D、(5,3)8. 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )
A、108° B、82° C、72° D、62°6. 同时抛掷两枚质地均匀的硬币,两枚硬币全部正面向上的概率为( )A、 B、 C、 D、7. 在平面直角坐标系xOy中,线段AB的两个端点坐标分别为A(﹣1,﹣1),B(1,2),平移线段AB,得到线段A′B′,已知A′的坐标为(3,﹣1),则点B′的坐标为( )A、(4,2) B、(5,2) C、(6,2) D、(5,3)8. 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,点E是AB的中点,CD=DE=a,则AB的长为( )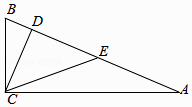 A、2a B、2 a C、3a D、
A、2a B、2 a C、3a D、二、填空题
-
9. 计算:﹣12÷3= .10. 下表是某校女子排球队队员的年龄分布:
年龄/岁
13
14
15
16
人数
1
4
5
2
则该校女子排球队队员年龄的众数是岁.
11. 五边形的内角和为 .12. 如图,在⊙O中,弦AB=8cm,OC⊥AB,垂足为C,OC=3cm,则⊙O的半径为 cm. 13. 关于x的方程x2+2x+c=0有两个不相等的实数根,则c的取值范围为 .14. 某班学生去看演出,甲种票每张30元,乙种票每张20元,如果36名学生购票恰好用去860元,设甲种票买了x张,乙种票买了y张,依据题意,可列方程组为 .15.
13. 关于x的方程x2+2x+c=0有两个不相等的实数根,则c的取值范围为 .14. 某班学生去看演出,甲种票每张30元,乙种票每张20元,如果36名学生购票恰好用去860元,设甲种票买了x张,乙种票买了y张,依据题意,可列方程组为 .15.如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为 n mile.(结果取整数,参考数据: ≈1.7, ≈1.4)
 16. 在平面直角坐标系xOy中,点A、B的坐标分别为(3,m)、(3,m+2),直线y=2x+b与线段AB有公共点,则b的取值范围为(用含m的代数式表示).
16. 在平面直角坐标系xOy中,点A、B的坐标分别为(3,m)、(3,m+2),直线y=2x+b与线段AB有公共点,则b的取值范围为(用含m的代数式表示).三、解答题
-
17. 计算:( +1)2﹣ +(﹣2)2 .18. 解不等式组: .19. 如图,在▱ABCD中,BE⊥AC,垂足E在CA的延长线上,DF⊥AC,垂足F在AC的延长线上,求证:AE=CF.
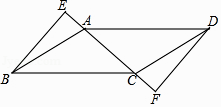 20. 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
20. 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.类别
A
B
C
D
E
节目类型
新闻
体育
动画
娱乐
戏曲
人数
12
30
m
54
9

请你根据以上的信息,回答下列问题:
(1)、被调查学生中,最喜爱体育节目的有人,这些学生数占被调查总人数的百分比为 %.(2)、被调查学生的总数为人,统计表中m的值为 , 统计图中n的值为 .(3)、在统计图中,E类所对应扇形的圆心角的度数为 .(4)、该校共有2000名学生,根据调查结果,估计该校最喜爱新闻节目的学生数.四、解答题
-
21. 某工厂现在平均每天比原计划多生产25个零件,现在生产600个零件所需时间与原计划生产450个零件所需时间相同,原计划平均每天生产多少个零件?22. 如图,在平面直角坐标系xOy中,双曲线y= 经过▱ABCD的顶点B,D.点D的坐标为(2,1),点A在y轴上,且AD∥x轴,S▱ABCD=5.
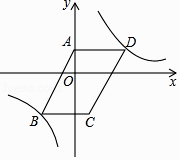 (1)、填空:点A的坐标为;(2)、求双曲线和AB所在直线的解析式.23. 如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.
(1)、填空:点A的坐标为;(2)、求双曲线和AB所在直线的解析式.23. 如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.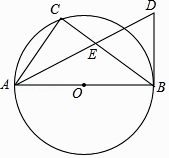 (1)、求证:BD=BE;(2)、若DE=2,BD= ,求CE的长.
(1)、求证:BD=BE;(2)、若DE=2,BD= ,求CE的长.五、解答题
-
24. 如图,在△ABC中,∠C=90°,AC=3,BC=4,点D,E分别在AC,BC上(点D与点A,C不重合),且∠DEC=∠A,将△DCE绕点D逆时针旋转90°得到△DC′E′.当△DC′E′的斜边、直角边与AB分别相交于点P,Q(点P与点Q不重合)时,设CD=x,PQ=y.
 (1)、求证:∠ADP=∠DEC;(2)、求y关于x的函数解析式,并直接写出自变量x的取值范围.25.
(1)、求证:∠ADP=∠DEC;(2)、求y关于x的函数解析式,并直接写出自变量x的取值范围.25.如图1,四边形ABCD的对角线AC,BD相交于点O,OB=OD,OC=OA+AB,AD=m,BC=n,∠ABD+∠ADB=∠ACB.
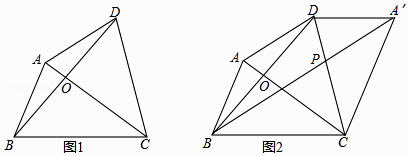 (1)、填空:∠BAD与∠ACB的数量关系为;(2)、求 的值;(3)、将△ACD沿CD翻折,得到△A′CD(如图2),连接BA′,与CD相交于点P.若CD= ,求PC的长.26. 在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,且经过点A(0, )(1)、若此抛物线经过点B(2,﹣ ),且与x轴相交于点E,F.
(1)、填空:∠BAD与∠ACB的数量关系为;(2)、求 的值;(3)、将△ACD沿CD翻折,得到△A′CD(如图2),连接BA′,与CD相交于点P.若CD= ,求PC的长.26. 在平面直角坐标系xOy中,抛物线y=ax2+bx+c的开口向上,且经过点A(0, )(1)、若此抛物线经过点B(2,﹣ ),且与x轴相交于点E,F.①填空:b=(用含a的代数式表示);
(2)、若a= ,当0<x<1,抛物线上的点到x轴距离的最大值为3时,求b的值.