2017年黑龙江省绥化市中考数学试卷

试卷更新日期：2017-07-13 类型：中考真卷

进入出卷网下载

一、选择题

1. 如图，直线AB，CD被直线EF所截，∠1=55°，下列条件中能判定AB∥CD的是（）

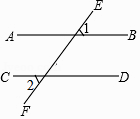A、∠2=35° B、∠2=45° C、∠2=55° D、∠2=125°

查看试题解析
2. 某企业的年收入约为700000元，数据“700000”用科学记数法可表示为（）

A、0.7×10⁶ B、7×10⁵ C、7×10⁴ D、70×10⁴

查看试题解析
3. 下列运算正确的是（）

A、3a+2a=5a² B、3a+3b=3ab C、2a²bc﹣a²bc=a²bc D、a⁵﹣a²=a³

查看试题解析
4. 正方形的正投影不可能是（）

A、线段 B、矩形 C、正方形 D、梯形

查看试题解析
5. 不等式组 ${\begin{matrix} x - 1 \leq 3 \\ x + 1 > 3 \end{matrix}$ 的解集是（）

A、x≤4 B、2＜x≤4 C、2≤x≤4 D、x＞2

查看试题解析
6. 如图，△A′B′C′是△ABC以点O为位似中心经过位似变换得到的，若△A′B′C′的面积与△ABC的面积比是4：9，则OB′：OB为（）

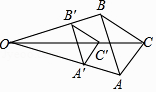A、2：3 B、3：2 C、4：5 D、4：9

查看试题解析
7. 从一副洗匀的普通扑克牌中随机抽取一张，则抽出红桃的概率是（）

A、 $\frac{1}{54}$ B、 $\frac{13}{54}$ C、 $\frac{1}{13}$ D、 $\frac{1}{4}$

查看试题解析
8. 在同一平面直角坐标系中，直线y=4x+1与直线y=﹣x+b的交点不可能在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9.
某楼梯的侧面如图所示，已测得BC的长约为3.5米，∠BCA约为29°，则该楼梯的高度AB可表示为（）

A、3.5sin29°米 B、3.5cos29°米 C、3.5tan29°米 D、 $\frac{3.5}{c o s 29 °}$ 米

查看试题解析
10. 如图，在▱ABCD中，AC，BD相交于点O，点E是OA的中点，连接BE并延长交AD于点F，已知S_△AEF=4，则下列结论：① $\frac{A F}{F D}$ = $\frac{1}{2}$ ；②S_△BCE=36；③S_△ABE=12；④△AEF～△ACD，其中一定正确的是（）

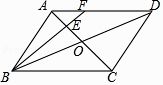A、①②③④ B、①④ C、②③④ D、①②③

查看试题解析

二、填空题

11. ﹣ $\frac{1}{5}$ 的绝对值是．

查看试题解析
12. 函数y= $\sqrt{2 - x}$ 中，自变量x的取值范围是．

查看试题解析
13. 一个多边形的内角和等于900°，则这个多边形是边形．

查看试题解析
14. 因式分解：x²﹣9= ．

查看试题解析
15. 计算：（ $\frac{a}{a + b}$ + $\frac{2 b}{a + b}$ ）• $\frac{a}{a + 2 b}$ = ．

查看试题解析
16. 一个扇形的半径为3cm，弧长为2πcm，则此扇形的面积为 cm²（用含π的式子表示）

查看试题解析
17. 在一次射击训练中，某位选手五次射击的环数分别为5，8，7，6，9，则这位选手五次射击环数的方差为．

查看试题解析
18. 半径为2的圆内接正三角形，正四边形，正六边形的边心距之比为．

查看试题解析
19. 已知反比例函数y= $\frac{6}{x}$ ，当x＞3时，y的取值范围是．

查看试题解析
20. 在等腰△ABC中，AD⊥BC交直线BC于点D，若AD= $\frac{1}{2}$ BC，则△ABC的顶角的度数为．

查看试题解析
21. 如图，顺次连接腰长为2的等腰直角三角形各边中点得到第1个小三角形，再顺次连接所得的小三角形各边中点得到第2个小三角形，如此操作下去，则第n个小三角形的面积为．

查看试题解析

三、解答题

22.
如图，A、B、C为某公园的三个景点，景点A和景点B之间有一条笔直的小路，现要在小路上建一个凉亭P，使景点B、景点C到凉亭P的距离之和等于景点B到景点A的距离，请用直尺和圆规在所给的图中作出点P．（不写作法和证明，只保留作图痕迹）

查看试题解析
23.
某校为了解学生每天参加户外活动的情况，随机抽查了100名学生每天参加户外活动的时间情况，并将抽查结果绘制成如图所示的扇形统计图．
请你根据图中提供的信息解答下列问题：

(1)、请直接写出图a的值，并求出本次抽查中学生每天参加户外活动时间的中位数；

(2)、求本次抽查中学生每天参加户外活动的平均时间．

查看试题解析
24. 已知关于x的一元二次方程x²+（2m+1）x+m²﹣4=0

(1)、当m为何值时，方程有两个不相等的实数根？

(2)、若边长为5的菱形的两条对角线的长分别为方程两根的2倍，求m的值．

查看试题解析
25. 甲、乙两个工程队计划修建一条长15千米的乡村公路，已知甲工程队每天比乙工程队每天多修路0.5千米，乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍．

(1)、求甲、乙两个工程队每天各修路多少千米？

(2)、若甲工程队每天的修路费用为0.5万元，乙工程队每天的修路费用为0.4万元，要使两个工程队修路总费用不超过5.2万元，甲工程队至少修路多少天？

查看试题解析
26. 如图，梯形ABCD中，AD∥BC，AE⊥BC于E，∠ADC的平分线交AE于点O，以点O为圆心，OA为半径的圆经过点B，交BC于另一点F．

(1)、求证：CD与⊙O相切；

(2)、若BF=24，OE=5，求tan∠ABC的值．

查看试题解析
27. 一辆轿车从甲城驶往乙城，同时一辆卡车从乙城驶往甲城，两车沿相同路线匀速行驶，轿车到达乙城停留一段时间后，按原路原速返回甲城；卡车到达甲城比轿车返回甲城早0.5小时，轿车比卡车每小时多行驶60千米，两车到达甲城弧均停止行驶，两车之间的路程y（千米）与轿车行驶时间t（小时）的函数图象如图所示，请结合图象提供的信息解答下列问题：

(1)、请直接写出甲城和乙城之间的路程，并求出轿车和卡车的速度；

(2)、求轿车在乙城停留的时间，并直接写出点D的坐标；

(3)、请直接写出轿车从乙城返回甲城过程中离甲城的路程s（千米）与轿车行驶时间t（小时）之间的函数关系式（不要求写出自变量的取值范围）．

查看试题解析
28. 如图，在矩形ABCD中，E为AB边上一点，EC平分∠DEB，F为CE的中点，连接AF，BF，过点E作EH∥BC分别交AF，CD于G，H两点．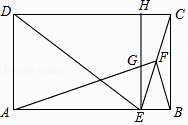

(1)、求证：DE=DC；

(2)、求证：AF⊥BF；

(3)、当AF•GF=28时，请直接写出CE的长．

查看试题解析
29.
在平面直角坐标系中，直线y=﹣ $\frac{3}{4}$ x+1交y轴于点B，交x轴于点A，抛物线y=﹣ $\frac{1}{2}$ x²+bx+c经过点B，与直线y=﹣ $\frac{3}{4}$ x+1交于点C（4，﹣2）．

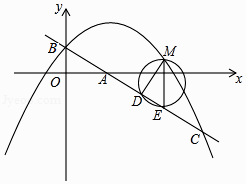(1)、求抛物线的解析式；

(2)、如图，横坐标为m的点M在直线BC上方的抛物线上，过点M作ME∥y轴交直线BC于点E，以ME为直径的圆交直线BC于另一点D，当点E在x轴上时，求△DEM的周长．

(3)、将△AOB绕坐标平面内的某一点按顺时针方向旋转90°，得到△A₁O₁B₁ ，点A，O，B的对应点分别是点A₁ ， O₁ ， B₁ ，若△A₁O₁B₁的两个顶点恰好落在抛物线上，请直接写出点A₁的坐标．

查看试题解析