2017年贵州省毕节地区中考数学试卷
试卷更新日期:2017-07-13 类型:中考真卷
一、选择题
-
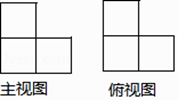
1. 下列实数中,无理数为( )A、0.2 B、 C、 D、22. 2017年毕节市参加中考的学生约为115000人,将115000用科学记数法表示为( )A、1.15×106 B、0.115×106 C、11.5×104 D、1.15×1053. 下列计算正确的是( )A、a3•a3=a9 B、(a+b)2=a2+b2 C、a2÷a2=0 D、(a2)3=a64. 一个几何体是由一些大小相同的小立方块摆成的,其主视图和俯视图如图所示,则组成这个几何体的小立方块最少有( )
 A、3个 B、4个 C、5个 D、6个5. 对一组数据:﹣2,1,2,1,下列说法不正确的是( )A、平均数是1 B、众数是1 C、中位数是1 D、极差是46. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=70°,则∠AED=( )
A、3个 B、4个 C、5个 D、6个5. 对一组数据:﹣2,1,2,1,下列说法不正确的是( )A、平均数是1 B、众数是1 C、中位数是1 D、极差是46. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=70°,则∠AED=( )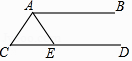 A、55° B、125° C、135° D、140°7. 关于x的一元一次不等式 ≤﹣2的解集为x≥4,则m的值为( )A、14 B、7 C、﹣2 D、28. 为估计鱼塘中的鱼的数量,可以先从鱼塘中随机打捞50条鱼,在每条鱼身上做上记号后,把这些鱼放归鱼塘,经过一段时间,等这些鱼完全混合于鱼群后,再从鱼塘中随机打捞50条鱼,发现只有2条鱼是前面做好记号的,那么可以估计这个鱼塘鱼的数量约为( )A、1250条 B、1750条 C、2500条 D、5000条9. 关于x的分式方程 +5= 有增根,则m的值为( )A、1 B、3 C、4 D、510. 甲、乙、丙、丁参加体育训练,近期10次跳绳测试的平均成绩都是每分钟174个,其方差如下表:
A、55° B、125° C、135° D、140°7. 关于x的一元一次不等式 ≤﹣2的解集为x≥4,则m的值为( )A、14 B、7 C、﹣2 D、28. 为估计鱼塘中的鱼的数量,可以先从鱼塘中随机打捞50条鱼,在每条鱼身上做上记号后,把这些鱼放归鱼塘,经过一段时间,等这些鱼完全混合于鱼群后,再从鱼塘中随机打捞50条鱼,发现只有2条鱼是前面做好记号的,那么可以估计这个鱼塘鱼的数量约为( )A、1250条 B、1750条 C、2500条 D、5000条9. 关于x的分式方程 +5= 有增根,则m的值为( )A、1 B、3 C、4 D、510. 甲、乙、丙、丁参加体育训练,近期10次跳绳测试的平均成绩都是每分钟174个,其方差如下表:选手
甲
乙
丙
丁
方差
0.023
0.018
0.020
0.021
则这10次跳绳中,这四个人发挥最稳定的是( )
A、甲 B、乙 C、丙 D、丁11. 把直线y=2x﹣1向左平移1个单位,平移后直线的关系式为( )A、y=2x﹣2 B、y=2x+1 C、y=2x D、y=2x+212. 如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD为( )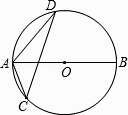 A、30° B、50° C、60° D、70°13. 如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF= CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )
A、30° B、50° C、60° D、70°13. 如图,Rt△ABC中,∠ACB=90°,斜边AB=9,D为AB的中点,F为CD上一点,且CF= CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )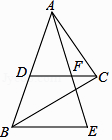 A、6 B、4 C、7 D、1214. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
A、6 B、4 C、7 D、1214. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( ) A、△AEE′是等腰直角三角形 B、AF垂直平分EE' C、△E′EC∽△AFD D、△AE′F是等腰三角形15.
A、△AEE′是等腰直角三角形 B、AF垂直平分EE' C、△E′EC∽△AFD D、△AE′F是等腰三角形15.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( )
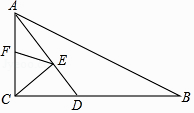 A、 B、 C、 D、6
A、 B、 C、 D、6二、填空题
-
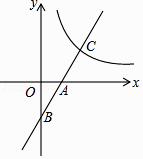
16. 分解因式:2x2﹣8xy+8y2= .17. 正六边形的边长为8cm,则它的面积为cm2 .18. 如图,已知一次函数y=kx﹣3(k≠0)的图象与x轴,y轴分别交于A,B两点,与反比例函数y= (x>0)交于C点,且AB=AC,则k的值为 .
 19. 记录某足球队全年比赛结果(“胜”、“负”、“平”)的条形统计图和扇形统计图(不完整)如下:
19. 记录某足球队全年比赛结果(“胜”、“负”、“平”)的条形统计图和扇形统计图(不完整)如下: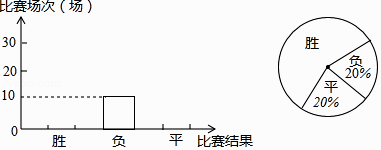
根据图中信息,该足球队全年比赛胜了场.
20. 观察下列运算过程:计算:1+2+22+…+210 .
解:设S=1+2+22+…+210 , ①
①×2得
2S=2+22+23+…+211 , ②
②﹣①得
S=211﹣1.
所以,1+2+22+…+210=211﹣1
运用上面的计算方法计算:1+3+32+…+32017= .
三、解答题
-
21. 计算:(﹣ )﹣2+(π﹣ )0﹣| ﹣ |+tan60°+(﹣1)2017 .22. 先化简,再求值:( + )÷ ,且x为满足﹣3<x<2的整数.23. 由于只有1张市运动会开幕式的门票,小王和小张都想去,两人商量采取转转盘(如图,转盘盘面被分为面积相等,且标有数字1,2,3,4的4个扇形区域)的游戏方式决定谁胜谁去观看.规则如下:两人各转动转盘一次,当转盘指针停止,如两次指针对应盘面数字都是奇数,则小王胜;如两次指针对应盘面数字都是偶数,则小张胜;如两次指针对应盘面数字是一奇一偶,视为平局.若为平局,继续上述游戏,直至分出胜负.
如果小王和小张按上述规则各转动转盘一次,则
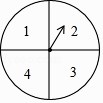 (1)、小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?(2)、该游戏是否公平?请用列表或画树状图的方法说明理由.24. 如图,在▱ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)、小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?(2)、该游戏是否公平?请用列表或画树状图的方法说明理由.24. 如图,在▱ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.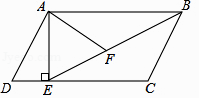 (1)、求证:△ABF∽△BEC;(2)、若AD=5,AB=8,sinD= ,求AF的长.25. 某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同.(1)、求这种笔和本子的单价;(2)、该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.26. 如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.
(1)、求证:△ABF∽△BEC;(2)、若AD=5,AB=8,sinD= ,求AF的长.25. 某同学准备购买笔和本子送给农村希望小学的同学,在市场上了解到某种本子的单价比某种笔的单价少4元,且用30元买这种本子的数量与用50元买这种笔的数量相同.(1)、求这种笔和本子的单价;(2)、该同学打算用自己的100元压岁钱购买这种笔和本子,计划100元刚好用完,并且笔和本子都买,请列出所有购买方案.26. 如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.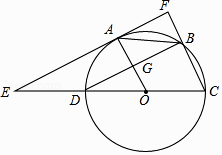 (1)、求证:EF是⊙O的切线;(2)、求AE的长.27.
(1)、求证:EF是⊙O的切线;(2)、求AE的长.27.如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
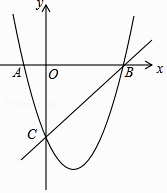 (1)、求这个二次函数的解析式;(2)、是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(1)、求这个二次函数的解析式;(2)、是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)、动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.