2017年广西河池市中考数学试卷
试卷更新日期:2017-07-13 类型:中考真卷
一、选择题
-
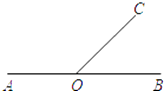
1. 下列实数中,为无理数的是( )A、﹣2 B、 C、2 D、42. 如图,点O在直线AB上,若∠BOC=60°,则∠AOC的大小是( )
 A、60° B、90° C、120° D、150°3. 若函数y= 有意义,则( )A、x>1 B、x<1 C、x=1 D、x≠14. 如图是一个由三个相同正方体组成的立体图形,它的主视图是( )
A、60° B、90° C、120° D、150°3. 若函数y= 有意义,则( )A、x>1 B、x<1 C、x=1 D、x≠14. 如图是一个由三个相同正方体组成的立体图形,它的主视图是( ) A、
A、 B、
B、 C、
C、 D、
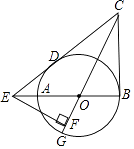
D、 5. 下列计算正确的是( )A、a3+a2=a5 B、a3•a2=a6 C、(a2)3=a6 D、a6÷a3=a26. 点P(﹣3,1)在双曲线y= 上,则k的值是( )A、﹣3 B、3 C、 D、7. 在《数据分析》章节测试中,“勇往直前”学习小组7位同学的成绩分别是92,88,95,93,96,95,94.这组数据的中位数和众数分别是( )A、94,94 B、94,95 C、93,95 D、93,968. 如图,⊙O的直径AB垂直于弦CD,∠CAB=36°,则∠BCD的大小是( )
5. 下列计算正确的是( )A、a3+a2=a5 B、a3•a2=a6 C、(a2)3=a6 D、a6÷a3=a26. 点P(﹣3,1)在双曲线y= 上,则k的值是( )A、﹣3 B、3 C、 D、7. 在《数据分析》章节测试中,“勇往直前”学习小组7位同学的成绩分别是92,88,95,93,96,95,94.这组数据的中位数和众数分别是( )A、94,94 B、94,95 C、93,95 D、93,968. 如图,⊙O的直径AB垂直于弦CD,∠CAB=36°,则∠BCD的大小是( )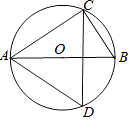 A、18° B、36° C、54° D、72°9. 三角形的下列线段中能将三角形的面积分成相等两部分的是( )A、中线 B、角平分线 C、高 D、中位线10. 若关于x的方程x2+2x﹣a=0有两个相等的实数根,则a的值为( )A、﹣1 B、1 C、﹣4 D、411. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )
A、18° B、36° C、54° D、72°9. 三角形的下列线段中能将三角形的面积分成相等两部分的是( )A、中线 B、角平分线 C、高 D、中位线10. 若关于x的方程x2+2x﹣a=0有两个相等的实数根,则a的值为( )A、﹣1 B、1 C、﹣4 D、411. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( ) A、6 B、8 C、10 D、1212. 已知等边△ABC的边长为12,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )A、3 B、4 C、8 D、9
A、6 B、8 C、10 D、1212. 已知等边△ABC的边长为12,D是AB上的动点,过D作DE⊥AC于点E,过E作EF⊥BC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )A、3 B、4 C、8 D、9二、填空题
-
13. 分解因式:x2﹣25= .14. 点A(2,1)与点B关于原点对称,则点B的坐标是 .15. 在校园歌手大赛中,参赛歌手的成绩为5位评委所给分数的平均分.各位评委给某位歌手的分数分别是92,93,88,87,90,则这位歌手的成绩是 .16. 如图,直线y=ax与双曲线y= (x>0)交于点A(1,2),则不等式ax> 的解集是 .
 17. 圆锥的底面半径长为5,将其侧面展开后得到一个半圆,则该半圆的半径长是 .18. 如图,在矩形ABCD中,AB= ,E是BC的中点,AE⊥BD于点F,则CF的长是 .
17. 圆锥的底面半径长为5,将其侧面展开后得到一个半圆,则该半圆的半径长是 .18. 如图,在矩形ABCD中,AB= ,E是BC的中点,AE⊥BD于点F,则CF的长是 .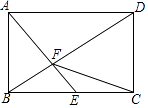
三、解答题
-
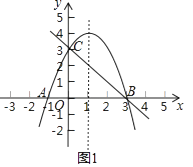
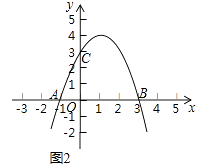
19. 计算:|﹣1|﹣2sin45°+ ﹣20 .20. 解不等式组: .21. 直线l的解析式为y=﹣2x+2,分别交x轴、y轴于点A,B.
 (1)、写出A,B两点的坐标,并画出直线l的图象;(2)、将直线l向上平移4个单位得到l1 , l1交x轴于点C.
(1)、写出A,B两点的坐标,并画出直线l的图象;(2)、将直线l向上平移4个单位得到l1 , l1交x轴于点C.①作出l1的图象,
②l1的解析式是 .
(3)、将直线l绕点A顺时针旋转90°得到l2 , l2交l1于点D.①作出l2的图象,
②tan∠CAD= .
22. 解答题(1)、如图1,在正方形ABCD中,点E,F分别在BC,CD上,AE⊥BF于点M,求证:AE=BF;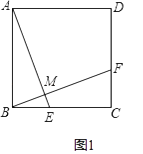 (2)、如图2,将 (1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE⊥BF于点M,探究AE与BF的数量关系,并证明你的结论.
(2)、如图2,将 (1)中的正方形ABCD改为矩形ABCD,AB=2,BC=3,AE⊥BF于点M,探究AE与BF的数量关系,并证明你的结论. 23. 九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
23. 九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”只是竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.频数分布表
分数段
频数(人数)
60≤x<70
a
70≤x<80
16
80≤x<90
24
90≤x<100
b
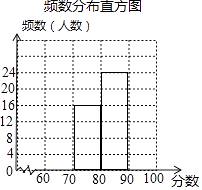
请解答下列问题:
(1)、完成频数分布表,a= , b= .(2)、补全频数分布直方图;(3)、全校共有600名学生参加初赛,估计该校成绩90≤x<100范围内的学生有多少人?(4)、九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.24. 某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多30元,用500元购得的排球数量与用800元购得的足球数量相等.(1)、排球和足球的单价各是多少元?(2)、若恰好用去1200元,有哪几种购买方案?