2017年浙江省杭州市中考数学试卷

试卷更新日期：2017-07-13 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣2²=（）

A、﹣2 B、﹣4 C、2 D、4

查看试题解析
2. 太阳与地球的平均距离大约是150 000 000千米，数据150 000 000用科学记数法表示为（）

A、1.5×10⁸ B、1.5×10⁹ C、0.15×10⁹ D、15×10⁷

查看试题解析
3.
如图，在△ABC中，点D，E分别在边AB，AC上，DE//BC，若BD=2AD，则（）

A、 $\frac{A D}{A B} = \frac{1}{2}$ B、 $\frac{A E}{E C} = \frac{1}{2}$ C、 $\frac{A D}{E C} = \frac{1}{2}$ D、 $\frac{D E}{B C} = \frac{1}{2}$

查看试题解析
4. |1+ $\sqrt{3}$ |+|1﹣ $\sqrt{3}$ |=（）

A、1 B、 $\sqrt{3}$ C、2 D、2 $\sqrt{3}$

查看试题解析
5. 设x，y，c是实数，（）

A、若x=y，则x+c=y﹣c B、若x=y，则xc=yc C、若x=y，则 $\frac{x}{c} = \frac{y}{c}$ D、若 $\frac{x}{2 c} = \frac{y}{3 c}$ ，则2x=3y

查看试题解析
6. 若x+5＞0，则（）

A、x+1＜0 B、x﹣1＜0 C、 $\frac{x}{5}$ ＜﹣1 D、﹣2x＜12

查看试题解析
7. 某景点的参观人数逐年增加，据统计，2014年为10.8万人次，2016年为16.8万人次．设参观人次的平均年增长率为x，则（）

A、10.8（1+x）=16.8 B、16.8（1﹣x）=10.8 C、10.8（1+x）²=16.8 D、10.8[（1+x）+（1+x）²]=16.8

查看试题解析
8.
如图，在Rt△ABC中，∠ABC=90°，AB=2，BC=1．把△ABC分别绕直线AB和BC旋转一周，所得几何体的地面圆的周长分别记作l₁ ， l₂ ，侧面积分别记作S₁ ， S₂ ，则（）

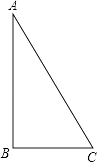A、l₁：l₂=1：2，S₁：S₂=1：2 B、l₁：l₂=1：4，S₁：S₂=1：2 C、l₁：l₂=1：2，S₁：S₂=1：4 D、l₁：l₂=1：4，S₁：S₂=1：4

查看试题解析
9. 设直线x=1是函数y=ax²+bx+c（a，b，c是实数，且a＜0）的图象的对称轴，（）

A、若m＞1，则（m﹣1）a+b＞0 B、若m＞1，则（m﹣1）a+b＜0 C、若m＜1，则（m﹣1）a+b＞0 D、若m＜1，则（m﹣1）a+b＜0

查看试题解析
10.
如图，在△ABC中，AB=AC，BC=12，E为AC边的中点，线段BE的垂直平分线交边BC于点D．设BD=x，tan∠ACB=y，则（）

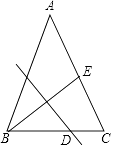A、x﹣y²=3 B、2x﹣y²=9 C、3x﹣y²=15 D、4x﹣y²=21

查看试题解析

二、填空题

11. 数据2，2，3，4，5的中位数是．

查看试题解析
12.
如图，AT切⊙O于点A，AB是⊙O的直径．若∠ABT=40°，则∠ATB= ．

查看试题解析
13. 一个仅装有球的不透明布袋里共有3个球（只有颜色不同），其中2个是红球，1个是白球，从中任意摸出一个球，记下颜色后放回，搅匀，再任意摸出一个球，则两次摸出都是红球的概率是．

查看试题解析
14. 若 $\frac{m - 3}{m - 1}$ •|m|= $\frac{m - 3}{m - 1}$ ，则m= ．

查看试题解析
15.
如图，在Rt△ABC中，∠BAC=90°，AB=15，AC=20，点D在边AC上，AD=5，DE⊥BC于点E，连结AE，则△ABE的面积等于．

查看试题解析
16. 某水果店销售50千克香蕉，第一天售价为9元/千克，第二天降为 6元/千克，第三天再降为3元/千克．三天全部售完，共计所得270元．若该店第二天销售香蕉t千克，则第三天销售香蕉千克．（用含t的代数式表示．）

查看试题解析

三、解答题

17.
为了了解某校九年级学生的跳高水平，随机抽取该年级50名学生进行跳高测试，并把测试成绩绘制成如图所示的频数表和未完成的频数直方图（每组含前一个边界值，不含后一个边界值）．
某校九年级50名学生跳高测试成绩的频数表
组别（m）
频数
1.09～1.19
8
1.19～1.29
12
1.29～1.39
A
1.39～1.49
10

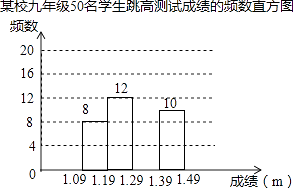(1)、求A的值，并把频数直方图补充完整；

(2)、该年级共有500名学生，估计该年级学生跳高成绩在1.29m（含1.29m）以上的人数．

查看试题解析
18. 在平面直角坐标系中，一次函数y=kx+b（k，b都是常数，且k≠0）的图象经过点（1，0）和（0，2）．

(1)、当﹣2＜x≤3时，求y的取值范围；

(2)、已知点P（m，n）在该函数的图象上，且m﹣n=4，求点P的坐标．

查看试题解析
19.
如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．

(1)、求证：△ADE∽△ABC；

(2)、若AD=3，AB=5，求 $\frac{A F}{A G}$ 的值．

查看试题解析
20. 在面积都相等的所有矩形中，当其中一个矩形的一边长为1时，它的另一边长为3．

(1)、设矩形的相邻两边长分别为x，y．
①求y关于x的函数表达式；
②当y≥3时，求x的取值范围；

(2)、圆圆说其中有一个矩形的周长为6，方方说有一个矩形的周长为10，你认为圆圆和方方的说法对吗？为什么？

查看试题解析
21.
如图，在正方形ABCD中，点G在对角线BD上（不与点B，D重合），GE⊥DC于点E，GF⊥BC于点F，连结AG．

(1)、写出线段AG，GE，GF长度之间的数量关系，并说明理由；

(2)、若正方形ABCD的边长为1，∠AGF=105°，求线段BG的长．

查看试题解析
22. 在平面直角坐标系中，设二次函数y₁=（x+a）（x﹣a﹣1），其中a≠0．

(1)、若函数y₁的图象经过点（1，﹣2），求函数y₁的表达式；

(2)、若一次函数y₂=ax+b的图象与y₁的图象经过x轴上同一点，探究实数a，b满足的关系式；

(3)、已知点P（x₀ ， m）和Q（1，n）在函数y₁的图象上，若m＜n，求x₀的取值范围．

查看试题解析
23.
如图，已知△ABC内接于⊙O，点C在劣弧AB上（不与点A，B重合），点D为弦BC的中点，DE⊥BC，DE与AC的延长线交于点E，射线AO与射线EB交于点F，与⊙O交于点G，设∠GAB=ɑ，∠ACB=β，∠EAG+∠EBA=γ，

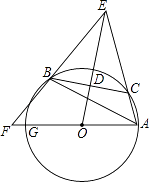(1)、点点同学通过画图和测量得到以下近似数据：
ɑ
30°
40°
50°
60°
β
120°
130°
140°
150°
γ
150°
140°
130°
120°
猜想：β关于ɑ的函数表达式，γ关于ɑ的函数表达式，并给出证明：

(2)、若γ=135°，CD=3，△ABE的面积为△ABC的面积的4倍，求⊙O半径的长．

查看试题解析

组别（m）	频数
1.09～1.19	8
1.19～1.29	12
1.29～1.39	A
1.39～1.49	10

ɑ	30°	40°	50°	60°
β	120°	130°	140°	150°
γ	150°	140°	130°	120°