2017年山东省青岛市中考数学试卷
试卷更新日期:2017-07-13 类型:中考真卷
一、选择题
-
1. ﹣ 的相反数是( )A、8 B、﹣8 C、 D、﹣2. 下列四个图形中,是轴对称图形,但不是中心对称图形的是( )A、
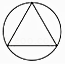 B、
B、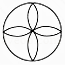 C、
C、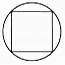 D、
D、 3. 小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法中错误的( )
3. 小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法中错误的( ) A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是4. 计算6m6÷(﹣2m2)3的结果为( )A、﹣m B、﹣1 C、 D、﹣5.
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是4. 计算6m6÷(﹣2m2)3的结果为( )A、﹣m B、﹣1 C、 D、﹣5.如图,若将△ABC绕点O逆时针旋转90°,则顶点B的对应点B1的坐标为( )
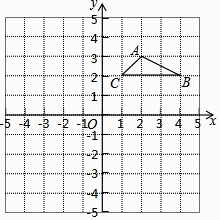 A、(﹣4,2) B、(﹣2,4) C、(4,﹣2) D、(2,﹣4)6. 如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )
A、(﹣4,2) B、(﹣2,4) C、(4,﹣2) D、(2,﹣4)6. 如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( ) A、100° B、110° C、115° D、120°7. 如图,▱ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB= ,AC=2,BD=4,则AE的长为( )
A、100° B、110° C、115° D、120°7. 如图,▱ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB= ,AC=2,BD=4,则AE的长为( ) A、 B、 C、 D、8. 一次函数y=kx+b(k≠0)的图象经过A(﹣1,﹣4),B(2,2)两点,P为反比例函数y= 图象上一动点,O为坐标原点,过点P作y轴的垂线,垂足为C,则△PCO的面积为( )A、2 B、4 C、8 D、不确定
A、 B、 C、 D、8. 一次函数y=kx+b(k≠0)的图象经过A(﹣1,﹣4),B(2,2)两点,P为反比例函数y= 图象上一动点,O为坐标原点,过点P作y轴的垂线,垂足为C,则△PCO的面积为( )A、2 B、4 C、8 D、不确定二、填空题
-
9. 近年来,国家重视精准扶贫,收效显著,据统计约65000000人脱贫,65000000用科学记数法可表示为 .10. 计算:( + )× = .11. 若抛物线y=x2﹣6x+m与x轴没有交点,则m的取值范围是 .12. 如图,直线AB,CD分别与⊙O相切于B,D两点,且AB⊥CD,垂足为P,连接BD,若BD=4,则阴影部分的面积为 .
 13. 如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为度.
13. 如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=58°,则∠EBD的度数为度. 14. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为 .
14. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为 .
三、解答题
-
15. 已知:四边形ABCD.
求作:点P,使∠PCB=∠B,且点P到边AD和CD的距离相等.
 16. 解答题(1)、解不等式组:(2)、化简:( ﹣a)÷ .17. 小华和小军做摸球游戏:A袋装有编号为1,2,3的三个小球,B袋装有编号为4,5,6的三个小球,两袋中的所有小球除编号外都相同.从两个袋子中分别随机摸出一个小球,若B袋摸出小球的编号与A袋摸出小球的编号之差为偶数,则小华胜,否则小军胜,这个游戏对双方公平吗?请说明理由.18. 某中学开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图,已知“查资料”的人数是40人.
16. 解答题(1)、解不等式组:(2)、化简:( ﹣a)÷ .17. 小华和小军做摸球游戏:A袋装有编号为1,2,3的三个小球,B袋装有编号为4,5,6的三个小球,两袋中的所有小球除编号外都相同.从两个袋子中分别随机摸出一个小球,若B袋摸出小球的编号与A袋摸出小球的编号之差为偶数,则小华胜,否则小军胜,这个游戏对双方公平吗?请说明理由.18. 某中学开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图,已知“查资料”的人数是40人.
请你根据以上信息解答下列问题:
(1)、在扇形统计图中,“玩游戏”对应的圆心角度数是度;(2)、补全条形统计图;(3)、该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数.19.如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈ ,cos67°≈ ,tan67°≈ , ≈1.73)
 20. A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发,图中l1 , l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
20. A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发,图中l1 , l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题: (1)、表示乙离A地的距离与时间关系的图象是(填l1或l2);
(1)、表示乙离A地的距离与时间关系的图象是(填l1或l2);甲的速度是km/h,乙的速度是km/h;
(2)、甲出发多少小时两人恰好相距5km?21. 已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF. (1)、求证:△BCE≌△DCF;(2)、当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.22. 青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间价格比淡季上涨 .下表是去年该酒店豪华间某两天的相关记录:
(1)、求证:△BCE≌△DCF;(2)、当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.22. 青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间价格比淡季上涨 .下表是去年该酒店豪华间某两天的相关记录:淡季
旺季
未入住房间数
10
0
日总收入(元)
24000
40000
(1)、该酒店豪华间有多少间?旺季每间价格为多少元?(2)、今年旺季来临,豪华间的间数不变.经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?23. 数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.(1)、探究一:求不等式|x﹣1|<2的解集
探究|x﹣1|的几何意义
如图①,在以O为原点的数轴上,设点A′对应的数是x﹣1,由绝对值的定义可知,点A′与点O的距离为|x﹣1|,可记为A′O=|x﹣1|.将线段A′O向右平移1个单位得到线段AB,此时点A对应的数是x,点B对应的数是1.因为AB=A′O,所以AB=|x﹣1|,因此,|x﹣1|的几何意义可以理解为数轴上x所对应的点A与1所对应的点B之间的距离AB.
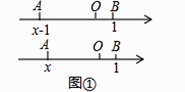
探究求方程|x﹣1|=2的解
因为数轴上3和﹣1所对应的点与1所对应的点之间的距离都为2,所以方程的解为3,﹣1.
探究:
求不等式|x﹣1|<2的解集
因为|x﹣1|表示数轴上x所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数x的范围.
请在图②的数轴上表示|x﹣1|<2的解集,并写出这个解集.
 (2)、
(2)、探究二:探究 的几何意义
探究:
的几何意义
如图③,在直角坐标系中,设点M的坐标为(x,y),过M作MP⊥x轴于P,作MQ⊥y轴于Q,则P点坐标为(x,0),Q点坐标为(0,y),OP=|x|,OQ=|y|,在Rt△OPM中,PM=OQ=|y|,则MO= = = ,因此, 的几何意义可以理解为点M(x,y)与点O(0,0)之间的距离MO.
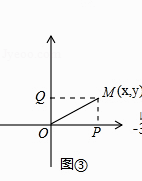
探究:
的几何意义
如图④,在直角坐标系中,设点A′的坐标为(x﹣1,y﹣5),由探究二(1)可知,A′O= ,将线段A′O先向右平移1个单位,再向上平移5个单位,得到线段AB,此时点A的坐标为(x,y),点B的坐标为(1,5),因为AB=A′O,所以AB= ,因此 的几何意义可以理解为点A(x,y)与点B(1,5)之间的距离AB.
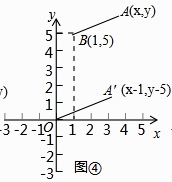
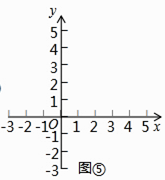
探究 的几何意义
①请仿照探究二的方法,在图⑤中画出图形,并写出探究过程.
② 的几何意义可以理解为:
 (3)、拓展应用:
(3)、拓展应用:① + 的几何意义可以理解为:点A(x,y)与点E(2,﹣1)的距离和点A(x,y)与点F(填写坐标)的距离之和.
② + 的最小值为(直接写出结果)
24.已知:Rt△EFP和矩形ABCD如图①摆放(点P与点B重合),点F,B(P),C在同一直线上,AB=EF=6cm,BC=FP=8cm,∠EFP=90°,如图②,△EFP从图①的位置出发,沿BC方向匀速运动,速度为1cm/s,EP与AB交于点G;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连接AF,FQ,当点Q停止运动时,△EFQ也停止运动.设运动时间为t(s)(0<t<6),解答下列问题:
 (1)、当t为何值时,PQ∥BD?(2)、设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使S五边形AFPQM:S矩形ABCD=9:8?若存在,求出t的值;若不存在,请说明理由.(4)、在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时,PQ∥BD?(2)、设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;(3)、在运动过程中,是否存在某一时刻t,使S五边形AFPQM:S矩形ABCD=9:8?若存在,求出t的值;若不存在,请说明理由.(4)、在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.