2017年山东省东营市中考数学试卷
试卷更新日期:2017-07-13 类型:中考真卷
一、选择题
-
1. 下列四个数中,最大的数是( )A、3 B、 C、0 D、π2. 下列运算正确的是( )A、(x﹣y)2=x2﹣y2 B、| ﹣2|=2﹣ C、﹣ = D、﹣(﹣a+1)=a+13. 若|x2﹣4x+4|与 互为相反数,则x+y的值为( )A、3 B、4 C、6 D、94. 小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,小明从家到学校行驶路程S(m)与时间t(min)的大致图象是( )
A、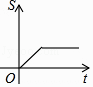 B、
B、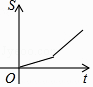 C、
C、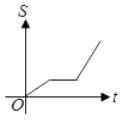 D、
D、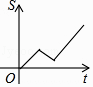 5. 已知a∥b,一块含30°角的直角三角板如图所示放置,∠2=45°,则∠1等于( )
5. 已知a∥b,一块含30°角的直角三角板如图所示放置,∠2=45°,则∠1等于( )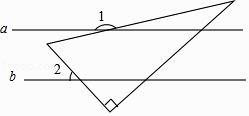 A、100° B、135° C、155° D、165°6. 如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )
A、100° B、135° C、155° D、165°6. 如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( ) A、 B、 C、 D、7. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=8,AB=5,则AE的长为( )
A、 B、 C、 D、7. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=8,AB=5,则AE的长为( ) A、5 B、6 C、8 D、128. 若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )A、60° B、90° C、120° D、180°9. 如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC= ,则△ABC移动的距离是( )
A、5 B、6 C、8 D、128. 若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )A、60° B、90° C、120° D、180°9. 如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC= ,则△ABC移动的距离是( ) A、 B、 C、 D、 ﹣10. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:
A、 B、 C、 D、 ﹣10. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH•PC
其中正确的是( )
 A、①②③④ B、②③ C、①②④ D、①③④
A、①②③④ B、②③ C、①②④ D、①③④二、填空题
-
11. 《“一带一路”贸易合作大数据报告(2017)》以“一带一路”贸易合作现状分析和趋势预测为核心,采集调用了8000多个种类,总计1.2亿条全球进出口贸易基础数据…,1.2亿用科学记数法表示为 .12. 分解因式:﹣2x2y+16xy﹣32y= .13. 为选拔一名选手参加全国中学生游泳锦标赛自由泳比赛,我市四名中学生参加了男子100米自由泳训练,他们成绩的平均数 及其方差s2如下表所示:
甲
乙
丙
丁
1′05″33
1′04″26
1′04″26
1′07″29
S2
1.1
1.1
1.3
1.6
如果选拔一名学生去参赛,应派去.
14. 如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CE•CO,其中正确结论的序号是 . 15.
15.如图,已知菱形ABCD的周长为16,面积为8 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
 16.
16.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是尺.
 17.
17.一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为米.
 18.
18.如图,在平面直角坐标系中,直线l:y= x﹣ 与x轴交于点B1 , 以OB1为边长作等边三角形A1OB1 , 过点A1作A1B2平行于x轴,交直线l于点B2 , 以A1B2为边长作等边三角形A2A1B2 , 过点A2作A2B3平行于x轴,交直线l于点B3 , 以A2B3为边长作等边三角形A3A2B3 , …,则点A2017的横坐标是 .

三、解答题
-
19. 计算题(1)、计算:6cos45°+( )﹣1+( ﹣1.73)0+|5﹣3 |+42017×(﹣0.25)2017(2)、先化简,再求值:( ﹣a+1)÷ + ﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.20. 为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,东营市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
 (1)、求该班的人数;(2)、请把折线统计图补充完整;(3)、求扇形统计图中,网络文明部分对应的圆心角的度数;(4)、小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.21. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F.
(1)、求该班的人数;(2)、请把折线统计图补充完整;(3)、求扇形统计图中,网络文明部分对应的圆心角的度数;(4)、小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.21. 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F. (1)、求证:DE⊥AC;(2)、若DE+EA=8,⊙O的半径为10,求AF的长度.22. 如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y= 的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3.
(1)、求证:DE⊥AC;(2)、若DE+EA=8,⊙O的半径为10,求AF的长度.22. 如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y= 的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3. (1)、求一次函数与反比例函数的解析式;(2)、直接写出当x>0时,kx+b﹣ <0的解集.23. 为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.(1)、改扩建1所A类学校和1所B类学校所需资金分别是多少万元?(2)、该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?24.
(1)、求一次函数与反比例函数的解析式;(2)、直接写出当x>0时,kx+b﹣ <0的解集.23. 为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.(1)、改扩建1所A类学校和1所B类学校所需资金分别是多少万元?(2)、该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?24.如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
 (1)、求证:△ABD∽△DCE;(2)、设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;(3)、当△ADE是等腰三角形时,求AE的长.25.
(1)、求证:△ABD∽△DCE;(2)、设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;(3)、当△ADE是等腰三角形时,求AE的长.25.如图,直线y=﹣ x+ 分别与x轴、y轴交于B、C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+ 经过A,B两点.
 (1)、求A、B两点的坐标;(2)、求抛物线的解析式;(3)、
(1)、求A、B两点的坐标;(2)、求抛物线的解析式;(3)、点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.
