2017年湖南省岳阳市中考数学试卷
试卷更新日期:2017-07-13 类型:中考真卷
一、选择题
-
1. 6的相反数是( )A、﹣6 B、 C、6 D、±62. 下列运算正确的是( )A、(x3)2=x5 B、(﹣x)5=﹣x5 C、x3•x2=x6 D、3x2+2x3=5x53. 据国土资源部数据显示,我国是全球“可燃冰”资源储量最多的国家之一,海、陆总储量约为39000000000吨油当量,将39000000000用科学记数法表示为( )A、3.9×1010 B、3.9×109 C、0.39×1011 D、39×1094. 下列四个立体图形中,主视图、左视图、俯视图都相同的是( )A、
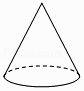 B、
B、 C、
C、 D、
D、 5. 从 ,0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是( )A、 B、 C、 D、6. 解分式方程 ﹣ =1,可知方程的解为( )A、x=1 B、x=3 C、x= D、无解7. 观察下列等式:21=2,22=4,23=8,24=16,25=32,26=64,…,根据这个规律,则21+22+23+24+…+22017的末位数字是( )A、0 B、2 C、4 D、68. 已知点A在函数y1=﹣ (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )A、有1对或2对 B、只有1对 C、只有2对 D、有2对或3对
5. 从 ,0,π,3.14,6这5个数中随机抽取一个数,抽到有理数的概率是( )A、 B、 C、 D、6. 解分式方程 ﹣ =1,可知方程的解为( )A、x=1 B、x=3 C、x= D、无解7. 观察下列等式:21=2,22=4,23=8,24=16,25=32,26=64,…,根据这个规律,则21+22+23+24+…+22017的末位数字是( )A、0 B、2 C、4 D、68. 已知点A在函数y1=﹣ (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )A、有1对或2对 B、只有1对 C、只有2对 D、有2对或3对二、填空题
-
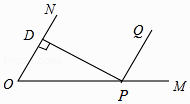
9. 函数y= 中自变量x的取值范围是 .10. 因式分解:x2﹣6x+9= .11. 在环保整治行动中,某市环保局对辖区内的单位进行了抽样调查,他们的综合得分如下:95,85,83,95,92,90,96,则这组数据的中位数是 , 众数是 .12. 如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是 .
 13. 不等式组 的解集是 .14. 在△ABC中BC=2,AB=2 ,AC=b,且关于x的方程x2﹣4x+b=0有两个相等的实数根,则AC边上的中线长为 .15. 我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值,设半径为r的圆内接正n边形的周长为L,圆的直径为d,如图所示,当n=6时,π≈ = =3,那么当n=12时,π≈ = . (结果精确到0.01,参考数据:sin15°=cos75°≈0.259)
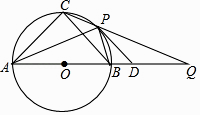
13. 不等式组 的解集是 .14. 在△ABC中BC=2,AB=2 ,AC=b,且关于x的方程x2﹣4x+b=0有两个相等的实数根,则AC边上的中线长为 .15. 我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值,设半径为r的圆内接正n边形的周长为L,圆的直径为d,如图所示,当n=6时,π≈ = =3,那么当n=12时,π≈ = . (结果精确到0.01,参考数据:sin15°=cos75°≈0.259) 16. 如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为弧 上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论正确的是 . (写出所有正确结论的序号)
16. 如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为弧 上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论正确的是 . (写出所有正确结论的序号)①若∠PAB=30°,则弧 的长为π;②若PD∥BC,则AP平分∠CAB;
③若PB=BD,则PD=6 ;④无论点P在弧 上的位置如何变化,CP•CQ为定值.
三、解答题
-
17. 计算:2sin60°+|3﹣ |+(π﹣2)0﹣( )﹣1 .18.
求证:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.

①已知:如图,在▱ABCD中,对角线AC,BD交于点O, .
②求证:
19. 如图,直线y=x+b与双曲线y= (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点. (1)、求直线和双曲线的解析式;(2)、点P在x轴上,且△BCP的面积等于2,求P点的坐标.20. 我市某校组织爱心捐书活动,准备将一批捐赠的书打包寄往贫困地区,其中每包书的数目相等.第一次他们领来这批书的 ,结果打了16个包还多40本;第二次他们把剩下的书全部取来,连同第一次打包剩下的书一起,刚好又打了9个包,那么这批书共有多少本?21. 为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:
(1)、求直线和双曲线的解析式;(2)、点P在x轴上,且△BCP的面积等于2,求P点的坐标.20. 我市某校组织爱心捐书活动,准备将一批捐赠的书打包寄往贫困地区,其中每包书的数目相等.第一次他们领来这批书的 ,结果打了16个包还多40本;第二次他们把剩下的书全部取来,连同第一次打包剩下的书一起,刚好又打了9个包,那么这批书共有多少本?21. 为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分如下:课外阅读时间(单位:小时)
频数(人数)
频率
0<t≤2
2
0.04
2<t≤4
3
0.06
4<t≤6
15
0.30
6<t≤8
a
0.50
t>8
5
b
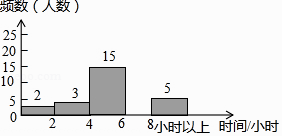
请根据图表信息回答下列问题:
(1)、频数分布表中的a= , b=;(2)、将频数分布直方图补充完整;(3)、学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”,请你估计该校2000名学生中评为“阅读之星”的有多少人?22. 某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.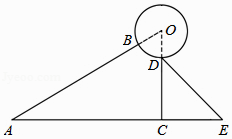 (1)、求支架CD的长;(2)、求真空热水管AB的长.(结果保留根号)23.
(1)、求支架CD的长;(2)、求真空热水管AB的长.(结果保留根号)23.问题背景:已知∠EDF的顶点D在△ABC的边AB所在直线上(不与A,B重合),DE交AC所在直线于点M,DF交BC所在直线于点N,记△ADM的面积为S1 , △BND的面积为S2 .
 (1)、初步尝试:如图①,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,则S1•S2=;(2)、类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图②所示位置,求S1•S2的值;(3)、
(1)、初步尝试:如图①,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,则S1•S2=;(2)、类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图②所示位置,求S1•S2的值;(3)、延伸拓展:当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α.
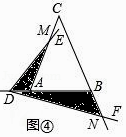
(Ⅰ)如图③,当点D在线段AB上运动时,设AD=a,BD=b,求S1•S2的表达式(结果用a,b和α的三角函数表示).
(Ⅱ)如图④,当点D在BA的延长线上运动时,设AD=a,BD=b,直接写出S1•S2的表达式,不必写出解答过程.

 24.
24.如图,抛物线y= x2+bx+c经过点B(3,0),C(0,﹣2),直线l:y=﹣ x﹣ 交y轴于点E,且与抛物线交于A,D两点,P为抛物线上一动点(不与A,D重合).
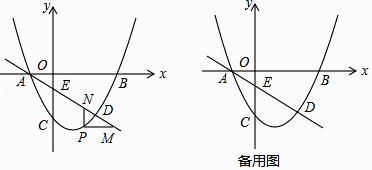 (1)、求抛物线的解析式;(2)、当点P在直线l下方时,过点P作PM∥x轴交l于点M,PN∥y轴交l于点N,求PM+PN的最大值.(3)、设F为直线l上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.
(1)、求抛物线的解析式;(2)、当点P在直线l下方时,过点P作PM∥x轴交l于点M,PN∥y轴交l于点N,求PM+PN的最大值.(3)、设F为直线l上的点,以E,C,P,F为顶点的四边形能否构成平行四边形?若能,求出点F的坐标;若不能,请说明理由.