2017年湖北省孝感市中考数学试卷
试卷更新日期:2017-07-13 类型:中考真卷
一、选择题
-
1. ﹣ 的绝对值是( )A、﹣3 B、3 C、 D、﹣2. 如图,直线a∥b,直线c与直线a,b分别交于点D,E,射线DF⊥直线c,则图中与∠1互余的角有( )
 A、4个 B、3个 C、2个 D、1个3. 下列计算正确的是( )A、b3•b3=2b3 B、(a+2)(a﹣2)=a2﹣4 C、(ab2)3=ab6 D、(8a﹣7b)﹣(4a﹣5b)=4a﹣12b4. 一个几何体的三视图如图所示,则这个几何体可能是( )
A、4个 B、3个 C、2个 D、1个3. 下列计算正确的是( )A、b3•b3=2b3 B、(a+2)(a﹣2)=a2﹣4 C、(ab2)3=ab6 D、(8a﹣7b)﹣(4a﹣5b)=4a﹣12b4. 一个几何体的三视图如图所示,则这个几何体可能是( )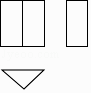 A、
A、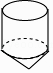 B、
B、 C、
C、 D、
D、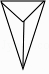 5. 不等式组 的解集在数轴上表示正确的是( )A、
5. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 方程 = 的解是( )A、x= B、x=5 C、x=4 D、x=﹣57. 下列说法正确的是( )A、调查孝感区居民对创建“全国卫生城市”的知晓度,宜采用抽样调查 B、一组数据85,95,90,95,95,90,90,80,95,90的众数为95 C、“打开电视,正在播放乒乓球比赛”是必然事件 D、同时抛掷两枚质地均匀的硬币一次,出现两个正面朝上的概率为8.
6. 方程 = 的解是( )A、x= B、x=5 C、x=4 D、x=﹣57. 下列说法正确的是( )A、调查孝感区居民对创建“全国卫生城市”的知晓度,宜采用抽样调查 B、一组数据85,95,90,95,95,90,90,80,95,90的众数为95 C、“打开电视,正在播放乒乓球比赛”是必然事件 D、同时抛掷两枚质地均匀的硬币一次,出现两个正面朝上的概率为8.如图,在平面直角坐标系中,点A的坐标为(﹣1, ),以原点O为中心,将点A顺时针旋转150°得到点A′,则点A′的坐标为( )
 A、(0,﹣2) B、(1,﹣ ) C、(2,0) D、( ,﹣1)9.
A、(0,﹣2) B、(1,﹣ ) C、(2,0) D、( ,﹣1)9.如图,在△ABC中,点O是△ABC的内心,连接OB,OC,过点O作EF∥BC分别交AB,AC于点E,F.已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
 A、
A、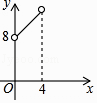 B、
B、 C、
C、 D、
D、 10.
10.如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )
①AB∥DE;②EF∥AD∥BC;③AF=CD;④四边形ACDF是平行四边形;⑤六边形ABCDEF既是中心对称图形,又是轴对称图形.
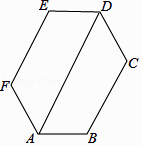 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
11. 我国是世界上人均拥有淡水量较少的国家,全国淡水资源的总量约为27500亿m3 , 应节约用水,数27500用科学记数法表示为 .12. 如图所示,图1是一个边长为a的正方形剪去一个边长为1的小正方形,图2是一个边长为(a﹣1)的正方形,记图1,图2中阴影部分的面积分别为S1 , S2 , 则 可化简为 .
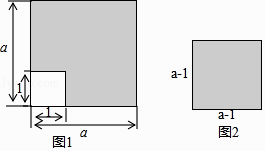 13.
13.如图,将直线y=﹣x沿y轴向下平移后的直线恰好经过点A(2,﹣4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为 .
 14. 如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段BH的长为 .
14. 如图,四边形ABCD是菱形,AC=24,BD=10,DH⊥AB于点H,则线段BH的长为 . 15. 已知半径为2的⊙O中,弦AC=2,弦AD=2 ,则∠COD的度数为 .16.
15. 已知半径为2的⊙O中,弦AC=2,弦AD=2 ,则∠COD的度数为 .16.如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y= (x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为 .

三、解答题
-
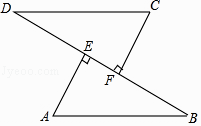
17. 计算:﹣22+ + •cos45°.18. 如图,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE,求证:AB∥CD.
 19. 今年四月份,某校在孝感市争创“全国文明城市”活动中,组织全体学生参加了“弘扬孝德文化,争做文明学生”的知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成A,B,C,D,E,F六个等级,并绘制成如下两幅不完整的统计图表.
19. 今年四月份,某校在孝感市争创“全国文明城市”活动中,组织全体学生参加了“弘扬孝德文化,争做文明学生”的知识竞赛,赛后随机抽取了部分参赛学生的成绩,按得分划分成A,B,C,D,E,F六个等级,并绘制成如下两幅不完整的统计图表.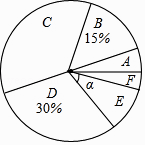
等级
得分x(分)
频数(人)
A
95≤x≤100
4
B
90≤x<95
m
C
85≤x<90
n
D
80≤x<85
24
E
75≤x<80
8
F
70≤x<75
4
请根据图表提供的信息,解答下列问题:
(1)、本次抽样调查样本容量为 , 表中:m= , n=;扇形统计图中,E等级对应扇形的圆心角α等于度;(2)、该校决定从本次抽取的A等级学生(记为甲、乙、丙、丁)中,随机选择2名成为学校文明宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
20.如图,已知矩形ABCD(AB<AD).
 (1)、请用直尺和圆规按下列步骤作图,保留作图痕迹;
(1)、请用直尺和圆规按下列步骤作图,保留作图痕迹;①以点A为圆心,以AD的长为半径画弧交边BC于点E,连接AE;
②作∠DAE的平分线交CD于点F;
③连接EF;
(2)、在(1)作出的图形中,若AB=8,AD=10,则tan∠FEC的值为 .21. 已知关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1 , x2 .(1)、求m的取值范围;(2)、若x1•x2满足3x1=|x2|+2,求m的值.22. 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有A,B两种型号的健身器材可供选择.(1)、劲松公司2015年每套A型健身器材的售价为2.5万元,经过连续两年降价,2017年每套售价为1.6万元,求每套A型健身器材年平均下降率n;(2)、2017年市政府经过招标,决定年内采购并安装劲松公司A,B两种型号的健身器材共80套,采购专项经费总计不超过112万元,采购合同规定:每套A型健身器材售价为1.6万元,每套B型健身器材售价为1.5(1﹣n)万元.①A型健身器材最多可购买多少套?
②安装完成后,若每套A型和B型健身器材一年的养护费分别是购买价的5%和15%,市政府计划支出10万元进行养护,问该计划支出能否满足一年的养护需要?
23. 如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD. (1)、由AB,BD, 围成的曲边三角形的面积是;(2)、求证:DE是⊙O的切线;(3)、求线段DE的长.24. 在平面直角坐标系xOy中,规定:抛物线y=a(x﹣h)2+k的伴随直线为y=a(x﹣h)+k.例如:抛物线y=2(x+1)2﹣3的伴随直线为y=2(x+1)﹣3,即y=2x﹣1.(1)、在上面规定下,抛物线y=(x+1)2﹣4的顶点坐标为 , 伴随直线为 , 抛物线y=(x+1)2﹣4与其伴随直线的交点坐标为和;(2)、
(1)、由AB,BD, 围成的曲边三角形的面积是;(2)、求证:DE是⊙O的切线;(3)、求线段DE的长.24. 在平面直角坐标系xOy中,规定:抛物线y=a(x﹣h)2+k的伴随直线为y=a(x﹣h)+k.例如:抛物线y=2(x+1)2﹣3的伴随直线为y=2(x+1)﹣3,即y=2x﹣1.(1)、在上面规定下,抛物线y=(x+1)2﹣4的顶点坐标为 , 伴随直线为 , 抛物线y=(x+1)2﹣4与其伴随直线的交点坐标为和;(2)、如图,顶点在第一象限的抛物线y=m(x﹣1)2﹣4m与其伴随直线相交于点A,B(点A在点B的左侧),与x轴交于点C,D.
①若∠CAB=90°,求m的值;
②如果点P(x,y)是直线BC上方抛物线上的一个动点,△PBC的面积记为S,当S取得最大值 时,求m的值.
