2017年湖北省襄阳市南漳县中考数学模拟试卷(5月份)
试卷更新日期:2017-07-13 类型:中考模拟
一、选择题
-
1. ﹣ 的相反数是( )A、2 B、﹣2 C、 D、﹣2. 中国的数学研究具有悠久的历史,《九章算术》是我国的一部古典数学名著,但对其成书的年代说法不一,一般认为在公元前后,距今约2 000年.将2 000用科学记数法表示为( )A、2×103 B、2×104 C、20×103 D、0.2×1033. 如图,小明同学将一个圆锥和一个三棱柱组成组合图形,观察其三视图,其俯视图是( )
 A、
A、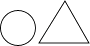 B、
B、 C、
C、 D、
D、 4. 如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDB的度数等于( )
4. 如图,点B是△ADC的边AD的延长线上一点,DE∥AC,若∠C=50°,∠BDE=60°,则∠CDB的度数等于( ) A、70° B、100° C、110° D、120°5. 某药品经过两次降价,每瓶零售价由168元降为128元.已知两次降价的百分率相同,每次降价的百分率为x,根据题意列方程得( )A、168(1+x)2=128 B、168(1﹣x)2=128 C、168(1﹣2x)=128 D、168(1﹣x2)=1286. 在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )A、16个 B、15个 C、13个 D、12个7. 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )
A、70° B、100° C、110° D、120°5. 某药品经过两次降价,每瓶零售价由168元降为128元.已知两次降价的百分率相同,每次降价的百分率为x,根据题意列方程得( )A、168(1+x)2=128 B、168(1﹣x)2=128 C、168(1﹣2x)=128 D、168(1﹣x2)=1286. 在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有( )A、16个 B、15个 C、13个 D、12个7. 如图,在⊙O中,弦AC∥半径OB,∠BOC=50°,则∠OAB的度数为( )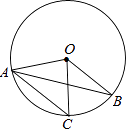 A、25° B、50° C、60° D、30°8. 若关于x的一元二次方程方程(k﹣1)x2+4x+1=0有实数根,则k的取值范围是( )A、k<5 B、k≥5,且k≠1 C、k≤5,且k≠1 D、k>59. 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac<0;②方程ax2+bx+c=0的两根之和大于0;③y随x的增大而增大;④a﹣b+c<0.其中正确的是( )
A、25° B、50° C、60° D、30°8. 若关于x的一元二次方程方程(k﹣1)x2+4x+1=0有实数根,则k的取值范围是( )A、k<5 B、k≥5,且k≠1 C、k≤5,且k≠1 D、k>59. 二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论:①ac<0;②方程ax2+bx+c=0的两根之和大于0;③y随x的增大而增大;④a﹣b+c<0.其中正确的是( ) A、①②③ B、②③④ C、①③④ D、①②④10. 如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
A、①②③ B、②③④ C、①③④ D、①②④10. 如图,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )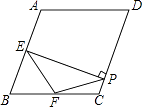 A、55° B、50° C、45° D、35°
A、55° B、50° C、45° D、35°二、填空题
-
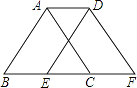
11. 因式分解:2a2﹣2= .12. 不等式组 的解集是 .13. 数据1,2,x,﹣1,﹣2的平均数是0,则这组数据的方差是 .14. 如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为 .
 15. 如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是(填出一个即可).
15. 如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是(填出一个即可). 16.
16.如图,△ABO中,AB⊥OB,OB= ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为 .

三、解答题.
-
17. 先化简,再求值:(m﹣n)2﹣(m+n)(m﹣n),其中m= +1,n= .18.
为弘扬中华优秀传统文化,今年2月20日举行了襄阳市首届中小学生经典诵读大赛决赛.某中学为了选拔优秀学生参加,广泛开展校级“经典诵读”比赛活动,比赛成绩评定为A,B,C,D,E五个等级,该校七(1)班全体学生参加了学校的比赛,并将比赛结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:
 (1)、该校七(1)班共有名学生;扇形统计图中C等级所对应扇形的圆心角等于度;(2)、补全条形统计图;(3)、若A等级的4名学生中有2名男生2名女生,现从中任意选取2名参加学校培训班,请用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.19. 如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD.
(1)、该校七(1)班共有名学生;扇形统计图中C等级所对应扇形的圆心角等于度;(2)、补全条形统计图;(3)、若A等级的4名学生中有2名男生2名女生,现从中任意选取2名参加学校培训班,请用列表法或画树状图的方法,求出恰好选到1名男生和1名女生的概率.19. 如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD. (1)、用尺规作图的方法,过点D作DM⊥BE,垂足为M(不写作法,只保留作图痕迹);(2)、若AB=2,求EM的长.20. 某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.(1)、求每行驶1千米纯用电的费用;(2)、若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?21. 如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象分别与x,y轴交于点B,A,与反比例函数y2= 的图象交于点C,D,CE⊥x轴于点E,tan∠ABO= ,OB=4,OE=2.
(1)、用尺规作图的方法,过点D作DM⊥BE,垂足为M(不写作法,只保留作图痕迹);(2)、若AB=2,求EM的长.20. 某种型号油电混合动力汽车,从A地到B地燃油行驶纯燃油费用76元,从A地到B地用电行驶纯电费用26元,已知每行驶1千米,纯燃油费用比纯用电费用多0.5元.(1)、求每行驶1千米纯用电的费用;(2)、若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元,则至少用电行驶多少千米?21. 如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象分别与x,y轴交于点B,A,与反比例函数y2= 的图象交于点C,D,CE⊥x轴于点E,tan∠ABO= ,OB=4,OE=2. (1)、求一次函数与反比例函数的解析式;(2)、根据图象直接写出当x<0且y1<y2时x的取值范围.22.
(1)、求一次函数与反比例函数的解析式;(2)、根据图象直接写出当x<0且y1<y2时x的取值范围.22.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC,垂足为F.
 (1)、求证:DF为⊙O的切线;(2)、若AE=4 ,∠CDF=22.5°,求阴影部分的面积.23. 某玩具专柜要经营一种新上市的儿童玩具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.(1)、写出专柜销售这种玩具,每天所得的销售利润W(元)与销售单价x(元)之间的函数关系式;(2)、求销售单价为多少元时,该玩具每天的销售利润最大;(3)、专柜结合上述情况,设计了A、B两种营销方案:
(1)、求证:DF为⊙O的切线;(2)、若AE=4 ,∠CDF=22.5°,求阴影部分的面积.23. 某玩具专柜要经营一种新上市的儿童玩具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.(1)、写出专柜销售这种玩具,每天所得的销售利润W(元)与销售单价x(元)之间的函数关系式;(2)、求销售单价为多少元时,该玩具每天的销售利润最大;(3)、专柜结合上述情况,设计了A、B两种营销方案:方案A:该玩具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件玩具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.
24.如图,△ABC中,∠ACB=90°,tanA= ,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
 (1)、求证:∠ADF=∠EDF;(2)、探究线段AD,AF,AB之间的数量关系,并说明理由;(3)、若EF=1,求BC的长.25.
(1)、求证:∠ADF=∠EDF;(2)、探究线段AD,AF,AB之间的数量关系,并说明理由;(3)、若EF=1,求BC的长.25.已知二次函数y=﹣x2+ax+b的图象与y轴交于点A(0,﹣2),与x轴交于点B(1,0)和点C,D(m,0)(m>2)是x轴上一点.
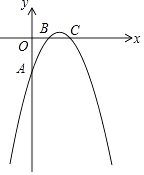 (1)、求二次函数的解析式;(2)、点E是第四象限内的一点,若以点D为直角顶点的Rt△CDE与以A,O,B为顶点的三角形相似,求点E坐标(用含m的代数式表示);(3)、在(2)的条件下,抛物线上是否存在一点F,使得四边形BCEF为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.
(1)、求二次函数的解析式;(2)、点E是第四象限内的一点,若以点D为直角顶点的Rt△CDE与以A,O,B为顶点的三角形相似,求点E坐标(用含m的代数式表示);(3)、在(2)的条件下,抛物线上是否存在一点F,使得四边形BCEF为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.