2017年黑龙江省哈尔滨市松北区中考数学二模试卷
试卷更新日期:2017-07-13 类型:中考模拟
一、选择题
-
1. ﹣3的倒数是( )A、3 B、 C、﹣3 D、﹣2. 下列运算错误的是( )A、(﹣a3)2=a6 B、a2+3a2=4a2 C、2a3•3a2=6a5 D、3a3÷2a=a23. 如图是由5个相同大小的正方体搭成的几何体,则它的俯视图是( )
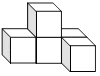 A、
A、 B、
B、 C、
C、 D、
D、 4. 国际数学家大会的会标如图1所示,把这个图案沿图中线段剪开后,能拼成如图2所示的四个图形,则其中是轴对称图形的有( )
4. 国际数学家大会的会标如图1所示,把这个图案沿图中线段剪开后,能拼成如图2所示的四个图形,则其中是轴对称图形的有( ) A、1个 B、2个 C、3个5. 一次函数y=-3x+2的图象不经过( )A、第一象限; B、第二象限; C、第三象限; D、第四象限.6. 不等式组 的解在数轴上表示为( )A、
A、1个 B、2个 C、3个5. 一次函数y=-3x+2的图象不经过( )A、第一象限; B、第二象限; C、第三象限; D、第四象限.6. 不等式组 的解在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 7. 合作交流是学习数学的重要方式之一,某校九年级每个班合作学习小组的个数分别是:8,7,7,8,9,7,这组数据的众数是( )A、7 B、7.5 C、8 D、98. 下列多边形中,内角和与外角和相等的是( )A、四边形 B、五边形 C、六边形 D、八边形9. 已知将二次函数y=x2+bx+c的图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣4x﹣5,则b,c的值为( )A、b=0,c=6 B、b=0,c=﹣5 C、b=0,c=﹣6 D、b=0.c=510. 甲、乙两人相约登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息,下列说法正确的个数为( )
7. 合作交流是学习数学的重要方式之一,某校九年级每个班合作学习小组的个数分别是:8,7,7,8,9,7,这组数据的众数是( )A、7 B、7.5 C、8 D、98. 下列多边形中,内角和与外角和相等的是( )A、四边形 B、五边形 C、六边形 D、八边形9. 已知将二次函数y=x2+bx+c的图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣4x﹣5,则b,c的值为( )A、b=0,c=6 B、b=0,c=﹣5 C、b=0,c=﹣6 D、b=0.c=510. 甲、乙两人相约登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息,下列说法正确的个数为( )(1 )甲登山上升的速度是每分钟10米;(2)乙在A地时距地面的高度b为30米;(3)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,乙登山1分钟时,距地面的高度为15米;(4)登山时间为4分钟,9分钟,15分钟时,甲、乙两人距地面的高度差为50米.
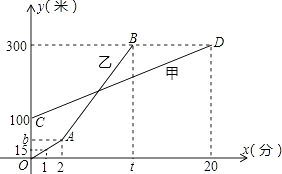 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 钓鱼诸岛是中国的固有领土,位于中国东海,面积约6344000平方米,数据6344000用科学记数法表示为 .12. 分解因式a2﹣ab2= .13. 函数y= 中自变量x的取值范围是 .14. 计算: = .15. 若方程kx2﹣6x+1=0有两个实数根,则k的取值范围是 .16. 如图,△ABC中,点D、E分别在边AB、BC上,DE∥AC.若BD=4,DA=2,BE=3,则EC= .
 17. 如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD= ﹣1,则∠ACD=°.
17. 如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD= ﹣1,则∠ACD=°. 18. 现有四张分别标有1,2,2,3的卡片,它们除数字外完全相同,把卡片背面向上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽出一张,则两次抽出的卡片所标数字不同的概率是 .19. 在矩形ABCD中,AD=5,AB=4,点E,F在直线AD上,且四边形BCFE为菱形.若线段EF的中点为点M,则线段AM的长为 .20. 如图,▱ABCD中,E是AB的中点,AB=10,AC=9,DE=12,则△CDE的面积S= .
18. 现有四张分别标有1,2,2,3的卡片,它们除数字外完全相同,把卡片背面向上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽出一张,则两次抽出的卡片所标数字不同的概率是 .19. 在矩形ABCD中,AD=5,AB=4,点E,F在直线AD上,且四边形BCFE为菱形.若线段EF的中点为点M,则线段AM的长为 .20. 如图,▱ABCD中,E是AB的中点,AB=10,AC=9,DE=12,则△CDE的面积S= .
三、解答题
-
21. 先化简,再求值: ,其中x=6tan30°﹣2.22.
平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.
 (1)、请写出旋转中心的坐标是 , 旋转角是度;(2)、以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形.23. 初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
(1)、请写出旋转中心的坐标是 , 旋转角是度;(2)、以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形.23. 初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题: (1)、在这次评价中,一共抽查了名学生;(2)、在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;(3)、请将频数分布直方图补充完整;(4)、如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人?24.
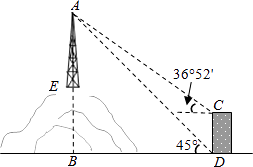
(1)、在这次评价中,一共抽查了名学生;(2)、在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为度;(3)、请将频数分布直方图补充完整;(4)、如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人?24.如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°,在楼顶C测得塔顶A的仰角36°52′.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.(参考数据:sin36°52′≈0.60,tan36°52′≈0.75)
 25. 某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)、该商家购进的第一批衬衫是多少件?(2)、若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?26. 如图,已知△ABC内接于⊙O,AD为边上的高,将△ADC沿直线AC翻折得到△AEC,延长EA交⊙O于点P,连接FC,交AB于N.
25. 某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.(1)、该商家购进的第一批衬衫是多少件?(2)、若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?26. 如图,已知△ABC内接于⊙O,AD为边上的高,将△ADC沿直线AC翻折得到△AEC,延长EA交⊙O于点P,连接FC,交AB于N. (1)、求证:∠BAC=∠ABC+∠ACF;(2)、求证:EF=DB;(3)、若AD=5,CD=10,CB∥AF,求点F到AB的距离.27.
(1)、求证:∠BAC=∠ABC+∠ACF;(2)、求证:EF=DB;(3)、若AD=5,CD=10,CB∥AF,求点F到AB的距离.27.如图,抛物线y=ax2﹣5ax﹣6a交x轴于A、B两点(A左B右),交y轴于点C,直线y=﹣x+b交抛物线于D,交x轴于E,且△ACE的面积为6.
 (1)、求抛物线的解析式;(2)、点P为CD上方抛物线上一点,过点P作x轴的平行线,交直线CD于F,设P点的横坐标为m,线段PF的长为d,求d与m的函数关系式;(3)、在(2)的条件下,过点P作PG⊥CD,垂足为G,若∠APG=∠ACO,求点P的坐标.
(1)、求抛物线的解析式;(2)、点P为CD上方抛物线上一点,过点P作x轴的平行线,交直线CD于F,设P点的横坐标为m,线段PF的长为d,求d与m的函数关系式;(3)、在(2)的条件下,过点P作PG⊥CD,垂足为G,若∠APG=∠ACO,求点P的坐标.