2017年河南省焦作市中考数学一模试卷

试卷更新日期：2017-07-13 类型：中考模拟

进入出卷网下载

一、选择题

1. $- \frac{1}{5}$ 的绝对值是（）

A、5 B、 $\frac{1}{5}$ C、 $- \frac{1}{5}$ D、﹣5

查看试题解析
2. 据河南省发改委发布消息，2016年全省固定资产投资继续保持持续稳定增长，全年完成39753亿元，总量居全国第3位．将数据39753亿用科学记数法表示为（）

A、3.9753×10⁹ B、0.39753×10¹⁰ C、39.753×10¹¹ D、3.9753×10¹²

查看试题解析
3. 如图，是由7个大小相同的小正方体堆砌而成的几何体，若从标有①、②、③、④的四个小正方体中取走一个后，余下几何体与原几何体的主视图相同，则取走的正方体是（）

A、① B、② C、③ D、④

查看试题解析
4. 下列计算正确的是（）

A、2a+3b=5ab B、（﹣a²）³=a⁶ C、（a+b）²=a²+b² D、 $\sqrt{8} - 2 \sqrt{2} = 0$

查看试题解析
5. 在一个不透明的袋子里装有两个红球和两个黄球，它们除颜色外都相同，随机从中摸出一球，记下颜色后放回袋中，充分摇匀后，再随机摸出一球，两次都摸到黄球的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
6. 要判断小强同学的数学考试成绩是否稳定，那么需要知道他最近几次数学考试成绩的（）

A、方差 B、众数 C、平均数 D、中位数

查看试题解析
7. 若关于x的一元二次方程（a﹣1）x²﹣2x+2=0有实数根，则整数a的最大值为（）

A、0 B、1 C、2 D、3

查看试题解析
8. 如图，在△ABC中，∠ABC=90°，∠A=30°，BC=4．若DE是△ABC的中位线，延长DE交∠ACM的平分线于点F，则DF的长为（）

A、6 B、7 C、8 D、9

查看试题解析
9. 如图，点A在双曲线y= $\frac{4}{x}$ 上，点B在双曲线y= $\frac{k}{x}$ （k≠0）上，AB∥x轴，分别过点A、B向x轴作垂线，垂足分别为D、C，若矩形ABCD的面积是9，则k的值为（）

A、4 B、5 C、9 D、13

查看试题解析
10. 如图，已知菱形ABCD的顶点A（﹣ $\sqrt{3}$ ，0），∠DAB=60°，若动点P从点A出发，沿A→B→C→D→A→B→…的路径，在菱形的边上以每秒0.5个单位长度的速度移动，则第2017秒时，点P的坐标为（）

A、 $(\frac{3 \sqrt{3}}{4} ， - \frac{1}{4})$ B、 $(- \frac{3 \sqrt{3}}{4} ， - \frac{1}{4})$ C、 $(- \sqrt{3} ， 0)$ D、 $(\sqrt{3} ， 0)$

查看试题解析

二、填空题

11. 计算：（﹣4）⁰﹣ $\sqrt{4}$ = ．

查看试题解析
12. 如图，在▱ABCD中，DB=DC，∠C=58°，AE⊥BD于E，则∠DAE=度．

查看试题解析
13. 在平面直角坐标系中，将抛物线y=（x﹣1）²先向上平移2个单位长度，再向右平移3个单位长度，得到的抛物线的解析式是．

查看试题解析
14. 如图，在圆心角为90°的扇形AOB中，半径OA=3，OC=AC，OD= $\frac{1}{2}$ BD，F是弧AB的中点．将△OCD沿CD折叠，点O落在点E处，则图中阴影部分的面积为．

查看试题解析
15. 如图，在△ABC中，∠C=90°，AB=5，BC=3，D是AB的中点，点E在边AC上，将△ADE沿DE翻折，使点A落在点A'处，当A'E⊥AC时，A'B= ．

查看试题解析

三、解答与证明

16. 先化简，再求值： $\frac{x^{2} - 2 x + 1}{2 x + 4}$ ÷（x﹣ $\frac{1 + 2 x}{x + 2}$ ），其中x是方程x²﹣4=0的根．

查看试题解析
17.
某校为了了解九年级学生（共450人）的身体素质情况，体育老师对九（1）班的50位学生进行一分钟跳绳次数测试，以测试数据为样本，绘制了如下部分频数分布表和部分频数分布直方图．
组别
次数x
频数（人数）
A
80≤x＜100
6
B
100≤x＜120
8
C
120≤x＜140
m
D
140≤x＜160
18
E
160≤x＜180
6
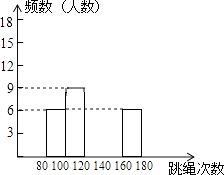
请结合图表解答下列问题：

(1)、表中的m=；

(2)、请把频数分布直方图补完整；

(3)、这个样本数据的中位数落在第组；

(4)、若九年级学生一分钟跳绳次数（x）合格要求是x≥120，则估计九年级学生中一分钟跳绳成绩不合格的人数．

查看试题解析
18.
如图，在△ABC中，以AB为直径的⊙O分别交AC，BC于点D，E．连接ED，若ED=EC．

(1)、求证：AB=AC；

(2)、填空：①若AB=6，CD=4，则BC=；
②连接OD，当∠A的度数为时，四边形ODEB是菱形．

查看试题解析
19. 南海是我国的南大门，如图所示，某天我国一艘海监执法船在南海海域正在进行常态化巡航，在A处测得北偏东30°方向上，距离为20海里的B处有一艘不明身份的船只正在向正东方向航行，便迅速沿北偏东75°的方向前往监视巡查，经过一段时间后，在C处成功拦截不明船只，问我海监执法船在前往监视巡查的过程中行驶了多少海里（最后结果保留整数）？
（参考数据：cos75°=0.2588，sin75°=0.9659，tan75°=3.732， $\sqrt{3}$ =1.732， $\sqrt{2}$ =1.414）

查看试题解析
20. 某学校计划购进A，B两种树木共100棵进行校园绿化升级，经市场调查：购买A种树木2棵，B种树木5棵，共需600元；购买A种树木3棵，B种树木1棵，共需380元．

(1)、求A种，B种树木每棵各多少元？

(2)、因布局需要，购买A种树木的数量不少于B种树木数量的3倍．学校与中标公司签订的合同中规定：在市场价格不变的情况下（不考虑其他因素），实际付款总金额按市场价九折优惠，请设计一种购买树木的方案，使实际所花费用最省，并求出最省的费用．

查看试题解析
21. 问题情境
已知矩形的面积为S（S为常数，S＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？
数学模型
设该矩形的长为x，周长为y，则y与x的函数关系式为y=2（x+ $\frac{S}{x}$ ）（x＞0）
探索研究

(1)、
我们可以借鉴学习函数的经验，先探索函数y=x+ $\frac{1}{x}$ （x＞0）的图象性质．
①列表：
x
…
   $\frac{1}{4}$
   $\frac{1}{3}$
   $\frac{1}{2}$
1
2
3
4
…
y
…
   $\frac{17}{4}$
m
   $\frac{5}{2}$
2
   $\frac{5}{2}$
   $\frac{10}{3}$
   $\frac{17}{4}$
…
表中m=；
②描点：如图所示；
③连线：请在图中画出该函数的图象；
④观察图象，写出两条函数的性质；

(2)、解决问题
在求二次函数y=ax²+bx+c（a≠0）的最大（小）值时，除了通过观察图象，还可以通过配方得到．同样通过配方也可以求函数y=x+ $\frac{1}{x}$ （x＞0）的最小值．
y=x+ $\frac{1}{x}$ = ${(\sqrt{x})}^{2}$ + ${(\sqrt{\frac{1}{x}})}^{2}$ = ${(\sqrt{x})}^{2}$ + ${(\sqrt{\frac{1}{x}})}^{2}$ ﹣2 $\sqrt{x}$ • $\sqrt{\frac{1}{x}}$ +2 $\sqrt{x}$ • $\sqrt{\frac{1}{x}}$ = $(\sqrt{x} - {\sqrt{\frac{1}{x})}}^{2}$ +2
∵ ${(\sqrt{x} - \sqrt{\frac{1}{x}})}^{2}$ ≥0，∴y≥2
∴当 $\sqrt{x}$ ﹣ $\sqrt{\frac{1}{x}}$ =0，即x=1时，y_最小值=2
请类比上面配方法，直接写出“问题情境”中的问题答案．

查看试题解析
22.
如图1，在Rt△ABC中，∠C=90°，AC=BC=2，点D、E分别在边AC、AB上，AD=DE= $\frac{1}{2}$ AB，连接DE．将△ADE绕点A逆时针方向旋转，记旋转角为θ．

(1)、问题发现
①当θ=0°时， $\frac{B E}{C D}$ =；
②当θ=180°时， $\frac{B E}{C D}$ = ．

(2)、
拓展探究
试判断：当0°≤θ＜360°时， $\frac{B E}{C D}$ 的大小有无变化？请仅就图2的情形给出证明；

(3)、问题解决
①在旋转过程中，BE的最大值为；
②当△ADE旋转至B、D、E三点共线时，线段CD的长为．

查看试题解析
23.
如图1，直线y= $\frac{3}{4}$ x+m与x轴、y轴分别交于点A和点B（0，﹣1），抛物线y= $\frac{1}{2}$ x²+bx+c经过点B，点C的横坐标为4．

(1)、请直接写出抛物线的解析式；

(2)、
如图2，点D在抛物线上，DE∥y轴交直线AB于点E，且四边形DFEG为矩形，设点D的横坐标为x（0＜x＜4），矩形DFEG的周长为l，求l与x的函数关系式以及l的最大值；

(3)、将△AOB绕平面内某点M旋转90°或180°，得到△A₁O₁B₁ ，点A、O、B的对应点分别是点A₁、O₁、B₁ ．若△A₁O₁B₁的两个顶点恰好落在抛物线上，那么我们就称这样的点为“落点”，请直接写出“落点”的个数和旋转180°时点A₁的横坐标．

查看试题解析

组别	次数x	频数（人数）
A	80≤x＜100	6
B	100≤x＜120	8
C	120≤x＜140	m
D	140≤x＜160	18
E	160≤x＜180	6

x	…	$\frac{1}{4}$	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	4	…
y	…	$\frac{17}{4}$	m	$\frac{5}{2}$	2	$\frac{5}{2}$	$\frac{10}{3}$	$\frac{17}{4}$	…