2017年广东省汕头市潮南区中考数学模拟试卷(5月份)
试卷更新日期:2017-07-13 类型:中考模拟
一、选择题
-
1. ﹣ 的相反数是( )A、3 B、﹣3 C、 D、﹣2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、a2+a2=a4 B、a6÷a2=a4 C、(a2)3=a5 D、(a﹣b)2=a2﹣b24.
3. 下列计算正确的是( )A、a2+a2=a4 B、a6÷a2=a4 C、(a2)3=a5 D、(a﹣b)2=a2﹣b24.如图,直线l1//l2 , 等腰直角△ABC的两个顶点A、B分别落在直线l1、l2上,∠ACB=90°,若∠1=15°,则∠2的度数是( )
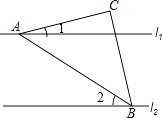 A、35° B、30° C、25° D、20°5. 据报道,2016年汕头市固定资产投资总额、社会消费品零售总额均突破1500亿元,将1500亿用科学记数法可表示为( )A、1.5×1011 B、1.5×1012 C、15×1011 D、0.15×10126. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ,则阴影部分的面积为( )
A、35° B、30° C、25° D、20°5. 据报道,2016年汕头市固定资产投资总额、社会消费品零售总额均突破1500亿元,将1500亿用科学记数法可表示为( )A、1.5×1011 B、1.5×1012 C、15×1011 D、0.15×10126. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ,则阴影部分的面积为( )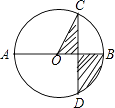 A、2π B、π C、 D、7. 不等式组 的解集在数轴上表示为( )A、
A、2π B、π C、 D、7. 不等式组 的解集在数轴上表示为( )A、 B、
B、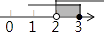 C、
C、 D、
D、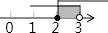 8. 一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )A、3,3,0.4 B、2,3,2 C、3,2,0.4 D、3,3,29. 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为( )
8. 一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )A、3,3,0.4 B、2,3,2 C、3,2,0.4 D、3,3,29. 如图,在△ABC中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点A落在BC边上的点D处,EF为折痕,若AE=3,则sin∠BFD的值为( )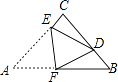 A、 B、 C、 D、10.
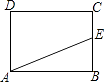
A、 B、 C、 D、10.如图,矩形ABCD中,AB=4,BC=3,动点E从B点出发,沿B﹣C﹣D﹣A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数关系用图象表示正确的是( )
 A、
A、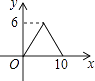 B、
B、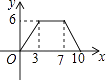 C、
C、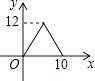 D、
D、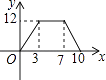
二、填空题
-
11. 若式子有意义,则x的取值范围是12. 因式分解:a2b﹣ab+ b= .13. 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为30°,测得底部C的俯角为60°,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为米(精确到1米,参考数据: ≈1.73).
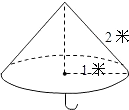
 14.
14.如图,一把遮阳伞撑开时母线的长是2米,底面半径为1米,则做这把遮阳伞需用布料的面积是 m2(结果保留π)
 15. 如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .
15. 如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .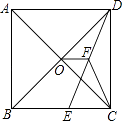 16. 一列数a1 , a2 , a3 , …满足条件:a1= ,an= (n≥2,且n为整数),则a2017= .
16. 一列数a1 , a2 , a3 , …满足条件:a1= ,an= (n≥2,且n为整数),则a2017= .三、解答题
-
17. 计算:(﹣1)2017+π0﹣( )﹣1+ .18. 先化简,再求值:( ﹣x﹣1)÷ ,其中x= ,y= .19. 如图,已知△ABC,∠BAC=90°.
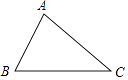 (1)、请用尺规作一条直线AD,使其将△ABC分成两个相似的三角形(保留作图痕迹,不写作法);(2)、直线AD与BC交于点D,若AB=3,AC=4,求线段AD的长.
(1)、请用尺规作一条直线AD,使其将△ABC分成两个相似的三角形(保留作图痕迹,不写作法);(2)、直线AD与BC交于点D,若AB=3,AC=4,求线段AD的长.四、解答题
-
20. 已知:如图,在▱ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
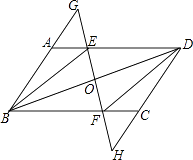 (1)、求证:△ABE≌△CDF;(2)、连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.21. 为了解市民对全市创卫工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.
(1)、求证:△ABE≌△CDF;(2)、连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.21. 为了解市民对全市创卫工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.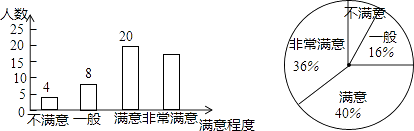
请结合图中信息,解决下列问题:
(1)、求此次调查中接受调查的人数.(2)、求此次调查中结果为非常满意的人数.(3)、兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.22. 在某节日前夕,几位同学到学校附近文具店调查一种进价为2元的节日贺卡的销售情况,每张定价3元,每天能卖出500张,每张售价每上涨0.1元,其每天销售量减少10个,另外,物价局规定,售价不得超过商品进价的240%,据此,请你解答下面问题:(1)、要实现每天800元的利润,应如何定价?(2)、800元的利润是否最大?如何定价,才能获得最大利润?五、解答题
-
23. 如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b和反比例函数y= 的图象的两个交点.
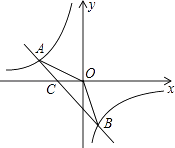 (1)、求一次函数和反比例函数的解析式;(2)、观察图象,直接写出不等式kx+b﹣ <0的解集;(3)、P是x轴上的一点,且满足△APB的面积是9,写出P点的坐标.24.
(1)、求一次函数和反比例函数的解析式;(2)、观察图象,直接写出不等式kx+b﹣ <0的解集;(3)、P是x轴上的一点,且满足△APB的面积是9,写出P点的坐标.24.如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC.
 (1)、判断直线l与⊙O的位置关系,并说明理由;(2)、若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)、在(2)的条件下,若DE=4,DF=3,求AF的长.25.
(1)、判断直线l与⊙O的位置关系,并说明理由;(2)、若∠ABC的平分线BF交AD于点F,求证:BE=EF;(3)、在(2)的条件下,若DE=4,DF=3,求AF的长.25.△ABC中,∠C=90°,∠A=60°,AC=2cm.长为1cm的线段MN在△ABC的边AB上沿AB方向以1cm/s的速度向点B运动(运动前点M与点A重合).过M,N分别作AB的垂线交直角边于P,Q两点,线段MN运动的时间为ts.
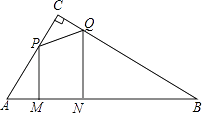 (1)、若△AMP的面积为y,写出y与t的函数关系式(写出自变量t的取值范围);
(1)、若△AMP的面积为y,写出y与t的函数关系式(写出自变量t的取值范围);
(2)、线段MN运动过程中,四边形MNQP有可能成为矩形吗?若有可能,求出此时t的值;若不可能,说明理由;(3)、t为何值时,以C,P,Q为顶点的三角形与△ABC相似?