2017年北京市中考数学押题试卷(5月份)
试卷更新日期:2017-07-13 类型:中考模拟
一、选择题
-
1. 转基因作物是利用基因工程将原有作物基因加入其它生物的遗传物质,并将不良基因移除,从而造成品质更好的作物.我国现有转基因作物种植面积约为4 200 000公顷,将4 200 000用科学记数法表示为( )A、4.2×106 B、4.2×105 C、42×105 D、0.42×1072.
如图,下列关于数m、n的说法正确的是( )
 A、m>n B、m=n C、m>﹣n D、m=﹣n3. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
A、m>n B、m=n C、m>﹣n D、m=﹣n3. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列运算中正确的是( )A、a2•a3=a5 B、(a2)3=a5 C、a6÷a2=a3 D、a5+a5=2a105. 某个密码锁的密码由三个数字组成,每个数字都是0﹣9这十个数字中的一个,只有当三个数字与所设定的密码及顺序完全相同时,才能将锁打开.如果仅忘记了锁设密码的最后那个数字,那么一次就能打开该密码的概率是( )A、 B、 C、 D、6.
4. 下列运算中正确的是( )A、a2•a3=a5 B、(a2)3=a5 C、a6÷a2=a3 D、a5+a5=2a105. 某个密码锁的密码由三个数字组成,每个数字都是0﹣9这十个数字中的一个,只有当三个数字与所设定的密码及顺序完全相同时,才能将锁打开.如果仅忘记了锁设密码的最后那个数字,那么一次就能打开该密码的概率是( )A、 B、 C、 D、6.如图,直线m∥n,将含有45°角的三角板ABC的直角顶点C放在直线n上,则∠1+∠2等于( )
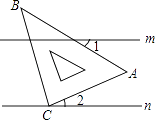 A、30° B、40° C、45° D、60°7. 一个多边形的内角和是外角和的3倍,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形8. 为了解居民用水情况,晓娜在某小区随机抽查了10户家庭的月用水量,结果如下表:
A、30° B、40° C、45° D、60°7. 一个多边形的内角和是外角和的3倍,则这个多边形是( )A、五边形 B、六边形 C、七边形 D、八边形8. 为了解居民用水情况,晓娜在某小区随机抽查了10户家庭的月用水量,结果如下表:月用水量(吨)
5
6
7
8
9
10
户数
1
1
2
2
3
1
则这10户家庭的月用水量的平均数和众数分别是( )
A、7.8,9 B、7.8,3 C、4.5,9 D、4.5,39. 如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,连接OC,若CD=6,OE=4,则OC等于( ) A、3 B、4 C、5 D、610.
A、3 B、4 C、5 D、610.已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).设四边形APFE的面积为y(cm2),则下列图象中,能表示y与t的函数关系的图象大致是( )
 A、
A、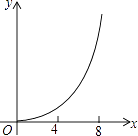 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 若分式 的值为0,则x的值等于 .12. 因式分解:﹣8ax2+16axy﹣8ay2= .13.
某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进10m到达点D处,又测得点A的仰角为60°,那么建筑物AB的高度是 m.
 14. 如图,在等腰三角形中,AB=AC,BC=4,D为BC的中点,点E、F在线段AD上,tan∠ABC=3,则阴影部分的面积是 .
14. 如图,在等腰三角形中,AB=AC,BC=4,D为BC的中点,点E、F在线段AD上,tan∠ABC=3,则阴影部分的面积是 . 15. 如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1 , △ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2 , △AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn= . (用含n的式子表示)
15. 如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1 , △ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2 , △AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn= . (用含n的式子表示)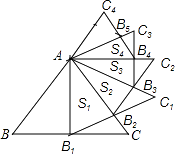 16. 阅读下面材料:
16. 阅读下面材料:在数学课上,老师请同学思考如下问题:

小轩的主要作法如下:

老师说:“小轩的作法正确.”
请回答:⊙P与BC相切的依据是 .
三、解答题
-
17. ﹣|﹣5|+3tan30°﹣ .18. 化简求值: ,其中a=2.19. 解不等式组: .20. 列方程或方程组解应用题:
为了响应市政府“绿色出行”的号召,小张上下班由自驾车方式改为骑自行车方式.已知小张单位与他家相距20千米,上下班高峰时段,自驾车的平均速度是自行平均车速度的2倍,骑自行车所用时间比自驾车所用时间多 小时.求自驾车平均速度和自行车平均速度各是多少?
21. 如图,一次函数y=x+1的图象与反比例函数 (k为常数,且k≠0)的图象都经过点A(m,2). (1)、求点A的坐标及反比例函数的表达式;(2)、设一次函数y=x+1的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.22. 已知关于x的一元二次方程x2+2x+k﹣2=0有两个不相等的实数根.(1)、求k的取值范围;(2)、若k为正整数,且该方程的根都是整数,求k的值.23. 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
(1)、求点A的坐标及反比例函数的表达式;(2)、设一次函数y=x+1的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.22. 已知关于x的一元二次方程x2+2x+k﹣2=0有两个不相等的实数根.(1)、求k的取值范围;(2)、若k为正整数,且该方程的根都是整数,求k的值.23. 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG. (1)、求证:四边形DEFG是平行四边形;(2)、如果∠OBC=45°,∠OCB=30°,OC=4,求EF的长.24. 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE.
(1)、求证:四边形DEFG是平行四边形;(2)、如果∠OBC=45°,∠OCB=30°,OC=4,求EF的长.24. 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,交AB于点E,过点D作DF⊥AB,垂足为F,连接DE. (1)、求证:直线DF与⊙O相切;(2)、若AE=7,BC=6,求AC的长.25. 为响应推进中小学生素质教育的号召,某校决定在下午15点至16点开设以下选修课:音乐史、管乐、篮球、健美操、油画.为了解同学们的选课情况,某班数学兴趣小组从全校三个年级中各调查一个班级,根据相关数据,绘制如下统计图.
(1)、求证:直线DF与⊙O相切;(2)、若AE=7,BC=6,求AC的长.25. 为响应推进中小学生素质教育的号召,某校决定在下午15点至16点开设以下选修课:音乐史、管乐、篮球、健美操、油画.为了解同学们的选课情况,某班数学兴趣小组从全校三个年级中各调查一个班级,根据相关数据,绘制如下统计图. (1)、请根据以上信息,直接补全条形统计图(图1)和扇形统计图(图2);(2)、若初一年级有180人,请估算初一年级中有多少学生选修音乐史?(3)、若该校共有学生540人,请估算全校有多少学生选修篮球课?26. 阅读下面材料:
(1)、请根据以上信息,直接补全条形统计图(图1)和扇形统计图(图2);(2)、若初一年级有180人,请估算初一年级中有多少学生选修音乐史?(3)、若该校共有学生540人,请估算全校有多少学生选修篮球课?26. 阅读下面材料:上课时李老师提出这样一个问题:对于任意实数x,关于x的不等式x2﹣2x﹣1﹣a>0恒成立,求a的取值范围.
小捷的思路是:原不等式等价于x2﹣2x﹣1>a,设函数y1=x2﹣2x﹣1,y2=a,画出两个函数的图象的示意图,于是原问题转化为函数y1的图象在y2的图象上方时a的取值范围.
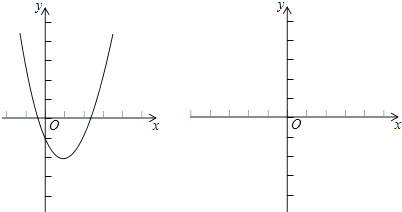 (1)、请结合小捷的思路回答:
(1)、请结合小捷的思路回答:对于任意实数x,关于x的不等式x2﹣2x﹣1﹣a>0恒成立,则a的取值范围是 .
(2)、参考小捷思考问题的方法,解决问题:关于x的方程x﹣4= 在0<a<4范围内有两个解,求a的取值范围.
27. 已知二次函数y=x2﹣2mx+m2+3(m是常数).(1)、求证:不论m为何值,该函数的图象与x轴没有公共点;(2)、把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?(3)、将抛物线y=x2﹣2mx+m2+3(m是常数)图象在对称轴左侧部分沿直线y=3翻折得到新图象为G,若与直线y=x+2有三个交点,请直接写出m的取值范围.28.如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
 (1)、求证:DE⊥AG;(2)、
(1)、求证:DE⊥AG;(2)、正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
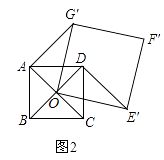
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
29. 在平面直角坐标系xOy中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S=ah.
例如:三点坐标分别为A(1,2),B(﹣3,1),C(2,﹣2),则“水平底”a=5,“铅垂高”h=4,“矩面积”S=ah=20.
(1)、已知点A(1,2),B(﹣3,1),P(0,t).①若A,B,P三点的“矩面积”为12,求点P的坐标;
②直接写出A,B,P三点的“矩面积”的最小值.
(2)、已知点E(4,0),F(0,2),M(m,4m),N(n, ),其中m>0,n>0.①若E,F,M三点的“矩面积”为8,求m的取值范围;
②直接写出E,F,N三点的“矩面积”的最小值及对应n的取值范围.