初中数学北师大版八年级上学期第五章 5.3 应用二元一次方程组-鸡兔同笼

试卷更新日期：2019-11-01 类型：同步测试

进入出卷网下载

一、单选题

1. 共20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵，设男生生有 $x$ 人,女生有 $y$ 人,根据题意,列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 52 \\ 3 x + 2 y = 20 \end{array}$ B、 ${\begin{array}{l} x + y = 52 \\ 2 x + 3 y = 20 \end{array}$ C、 ${\begin{array}{l} x + y = 20 \\ 3 x + 2 y = 52 \end{array}$ D、 ${\begin{array}{l} x + y = 20 \\ 2 x + 3 y = 52 \end{array}$

查看试题解析
2. 《九章算术》是中国古代重要的数学著作。其中“盈不足术”记载:今有共买鸡，人出九，盈十一;人出六，不足十六。问人数鸡价各几何?译文:今有人合伙买鸡，每人出9钱，会多出11钱;每人出6钱，又差16钱。问人数、买鸡的钱数各是多少?设人数为x，买鸡的钱数为y，可列方程组为（）

A、 ${\begin{cases} 9 x + 11 = y \\ 6 x + 16 = y \end{cases}$ B、 ${\begin{cases} 9 x - 11 = y \\ 6 x - 16 = y \end{cases}$ C、 ${\begin{cases} 9 x + 11 = y \\ 6 x - 16 = y \end{cases}$ D、 ${\begin{cases} 9 x - 11 = y \\ 6 x + 16 = y \end{cases}$

查看试题解析
3. 我校一批师生共1152人参加中考体育测试，现已预备了48座和32座的两种客车共30辆，刚好坐满．设48座客车x辆，32座客车y辆，根据题意，可以列出方程组（）

A、 ${\begin{cases} x + y = 1152 \\ 48 x + 32 y = 30 \end{cases}$ B、 ${\begin{cases} x + y = 1152 \\ 32 x + 48 y = 30 \end{cases}$ C、 ${\begin{cases} x + y = 30 \\ 32 x + 48 y = 1152 \end{cases}$ D、 ${\begin{cases} x + y = 30 \\ 48 x + 32 y = 1152 \end{cases}$

查看试题解析
4. 如果鸡和兔共15个头，46只脚，那么鸡有（）只.

A、6 B、7 C、8 D、9

查看试题解析
5. 据《九章算术》中记载：“鸡兔同笼不知数，三十六头笼中露，看来脚有100只，几多鸡儿几多兔？”，若设鸡 $x$ 只，兔 $y$ 只，则所列方程组是（）

A、 ${\begin{matrix} x + y = 36 \\ 2 x + 4 y = 100 \end{matrix}$ B、 ${\begin{matrix} x + y = 36 \\ 4 x + 2 y = 100 \end{matrix}$ C、 ${\begin{matrix} 2 x + 4 y = 36 \\ x + y = 100 \end{matrix}$ D、 ${\begin{matrix} 4 x + 2 y = 36 \\ x + y = 100 \end{matrix}$

查看试题解析
6. 《九章算术》是中国传统数学名著，其中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两．问牛、羊各直金几何？”译文：“假设有5头牛，2只羊，值金10两；2头牛，5只羊，值金8两．问每头牛、每只羊各值金多少两？”若设每头牛、每只羊分别值金x两、y两，则可列方程组为（）

A、 ${\begin{matrix} 5 x + 2 y = 10 \\ 2 x + 5 y = 8 \end{matrix}$ B、 ${\begin{matrix} 5 x - 2 y = 10 \\ 2 x - 5 y = 8 \end{matrix}$ C、 ${\begin{matrix} 5 x + 2 y = 10 \\ 2 x - 5 y = 8 \end{matrix}$ D、 ${\begin{matrix} 5 x + 2 y = 8 \\ 2 x + 5 y = 10 \end{matrix}$

查看试题解析

二、填空题

7. 我国古代数学著作《九章算术》中记载：“今有大器五小器一容三斛，大器一小器五容二斛.问大小器各容几何.”其大意为：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛（斛，音hu ，是古代的一种容量单位）.1个大桶加上5个小桶可以盛酒2斛，问1个大桶、一个小桶分别可以盛酒多少斛？若设1个大桶可以盛酒x斛，1个小桶可以盛酒y斛，根据题意，可列方程组为.

查看试题解析
8. 小林、小芳和小亮三人玩飞镖游戏，各投5支飞镖，规定在同一圆环内得分相同，中靶和得分情况如图，则小亮的得分是分．

查看试题解析

三、解答题

9. 为倡导市民绿色出行，提高市民环保意识和健康意识，怀柔区建立了城市公共自行车系统，共建64个站点，投放2300辆自行车.并于2016年8月15日正式投入运营.办理借车卡和借车服务费标准如下：
首次办理借车卡免收工本费，本地居民收取300元保证金及预充值消费50元、外地居民收取500元保证金及预充值消费50元.

借车服务费用实行分段合计，还车刷卡时，从借车卡中结算扣取，每次借车1小时（含）为免费租用期；超过免费租用期1小时以内（含）的收取1元；超过免费租用期2小时到4小时以内（含）的，每小时收取2元；超过免费租用期4个小时以上的，每小时收取3元；一天20元封顶（不足一小时按1小时计）.

刘亮妈妈到网点首次办了一张借车卡.第一次，她用了5小时20分钟后才还车.后来妈妈又借车出行了30次，卡中预充值的费用就全部用完了，妈妈说后来的这30次，每次从卡中扣除的服务费都是1元或3元.请你通过列方程或方程组的方法帮刘亮妈妈算一算她扣除1元和3元服务费各几次.

查看试题解析

四、综合题

10. 学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元；购买5个A奖品和4个B奖品共需210元.

(1)、求A，B两种奖品的单价；

(2)、学校准备购买A，B两种奖品共30个，且A奖品的数量不少于B奖品数量的 $\frac{1}{3}$ .请设计出最省钱的购买方案，并说明理由.

查看试题解析
11. 如图，杭州某化工厂与A，B两地有公路，铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂，制成每吨8000元的产品运到B地.已知公路运价为1.4元/（吨•千米），铁路运价为1.1元/（吨•千米），且这两次运输共支出公路运输费14000元，铁路运输费89100元，求：

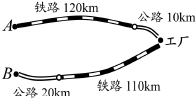(1)、该工厂从A地购买了多少吨原料？制成运往B地的产品多少吨？

(2)、这批产品的销售款比原料费与运输费的和多多少元？

查看试题解析

初中数学北师大版八年级上学期 第五章 5.3 应用二元一次方程组-鸡兔同笼

一、单选题

二、填空题

三、解答题

四、综合题

初中数学北师大版八年级上学期第五章 5.3 应用二元一次方程组-鸡兔同笼