备考2020年高考数学一轮复习：49 椭圆

试卷更新日期：2019-11-01 类型：一轮复习

进入出卷网下载

一、单选题

1. 椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{16}$ =1的焦点坐标是（）

A、(0，3)，(0，-3) B、(3，0)，(-3，0) C、(0， $\sqrt{41}$ )，(0，- $\sqrt{41}$ ) D、( $\sqrt{41}$ ，0)，(- $\sqrt{41}$ ，0)

查看试题解析
2. 已知椭圆 $C : \frac{x^{2}}{25} + \frac{y^{2}}{m^{2}} = 1 (m > 0)$ 的左、右焦点分别为 $F_{1}, F_{2}$ ，点 $P$ 在 $C$ 上，且 $Δ P F_{1} F_{2}$ 的周长为 $16$ ，则 $m$ 的值是（）

A、 $2$ B、 $3$ C、 $2 \sqrt{3}$ D、 $4$

查看试题解析
3. 若直线 $x - 2 y + 2 = 0$ 经过椭圆的一个焦点和一个顶点，则该椭圆的标准方程为（）

A、 $\frac{x^{2}}{5} + y^{2} = 1$ B、 $\frac{x^{2}}{4} + \frac{y^{2}}{5} = 1$ C、 $\frac{x^{2}}{5} + y^{2} = 1$ 或 $\frac{x^{2}}{4} + \frac{y^{2}}{5} = 1$ D、以上答案都不对

查看试题解析
4. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点为 $F$ ，短轴的一个端点为 $P$ ，直线 $l ： 4 x - 3 y = 0$ 与椭圆相交于 $A$ 、 $B$ 两点.若 $| A F | + | B F | = 6$ ，点 $P$ 到直线 $l$ 的距离不小于 $\frac{6}{5}$ ，则椭圆离心率的取值范围为（）

A、 $(0 ， \frac{9}{5}]$ B、 $(0 ， \frac{\sqrt{3}}{2}]$ C、 $(0 ， \frac{\sqrt{5}}{3}]$ D、 $(\frac{1}{3} ， \frac{\sqrt{3}}{2}]$

查看试题解析
5. 人造地球卫星绕地球运行遵循开普勒行星运动定律：卫星在以地球为焦点的椭圆轨道上绕地球运行时，其运行速度是变化的，速度的变化服从面积守恒规律，即卫星的向径(卫星至地球的连线)在相同的时间内扫过的面积相等.设椭圆的长轴长、焦距分别为 $2 a ， 2 c .$ 李明根据所学的椭圆知识，得到下列结论：

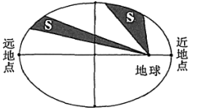
①卫星向径的最小值为 $a - c$ ，最大值为 $a + c$ ；②卫星向径的最小值与最大值的比值越小，椭圆轨道越扁；③卫星运行速度在近地点时最小，在远地点时最大其中正确结论的个数是（）

A、 $0$ B、 $1$ C、 $2$ D、 $3$

查看试题解析
6. 设椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a>b>0）的左，右焦点分别为F₁ ， F₂ ，离心率为 $\frac{\sqrt{5}}{3}$ ，以F₁F₂为直径的圆与C在第一象限的交点为P，则直线PF₁的斜率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
7. 设 $F$ 是椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点， $A$ 是椭圆 $E$ 的左顶点， $P$ 为直线 $x = \frac{3 a}{2}$ 上一点， $Δ A P F$ 是底角为 $30^{0}$ 的等腰三角形，则椭圆 $E$ 的离心率为（）

A、 $\frac{3}{4}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
8. 设 $P$ 是椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ 上一点， $F_{1}, F_{2}$ 是椭圆的焦点，若 $| P F_{1} | = 3$ ，则 $| P F_{2} |$ 等于（）

A、2 B、3 C、5 D、7

查看试题解析
9. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右顶点分别为A₁ ， A₂ ，且以线段A₁A₂为直径的圆与直线 $b x - a y + 2 a b = 0$ 相切，则C的离心率为（）

A、 $\frac{\sqrt{6}}{3}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{1}{3}$

查看试题解析
10. 已知椭圆 $\frac{x^{2}}{5} + \frac{y^{2}}{m} = 1$ 的离心率 $e = \frac{\sqrt{10}}{5}$ ，则 $m$ 的值为（）

A、3 B、3或 $\frac{25}{3}$ C、 $\sqrt{15}$ D、 $\sqrt{15}$ 或 $\frac{5}{3} \sqrt{15}$

查看试题解析
11. 正方形 $A B C D$ 的四个顶点都在椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ 上，若椭圆的焦点在正方形的内部，则椭圆的离心率的取值范围是（）

A、 $(\frac{\sqrt{5} - 1}{2}, 1)$ B、 $(0, \frac{\sqrt{5} - 1}{2})$ C、 $(\frac{\sqrt{3} - 1}{2}, 1)$ D、 $(0, \frac{\sqrt{3} - 1}{2})$

查看试题解析
12. 已知 $A B$ 是椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{5} = 1$ 的长轴，若把线段 $A B$ 五等份，过每个分点作 $A B$ 的垂线，分别与椭圆的上半部分相交于 $C$ 、 $D$ 、 $E$ 、 $G$ 四点，设 $F$ 是椭圆的左焦点，则 $| F C | + | F D | + | F E | + | F G |$ 的值是（）

A、 $15$ B、 $16$ C、 $18$ D、 $20$

查看试题解析

二、填空题

13. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点分别为 $F_{1}, F_{2}$ ，离心率为 $e$ ．若椭圆上存在点 $P$ ，使得 $\frac{| P F_{1} |}{| P F_{2} |} = e$ ，则该椭圆离心率 $e$ 的取值范围是．

查看试题解析
14. 已知椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{5} = 1$ 的左焦点为F，点P在椭圆且在x轴上方，若线段PF的中点在以原点O为圆心，|OF|为半径的圆上，则直线PF的斜率是

查看试题解析
15. 设F₁ ， F₂为椭圆C： $\frac{x^{2}}{36} + \frac{y^{2}}{20} = 1$ 的两个焦点，M为C上一点且在第一象限，若△MF₁F₂为等腰三角形，则M的坐标为。

查看试题解析
16. 设 $A, B$ 分别为椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右顶点和上顶点，已知椭圆 $C$ 过点 $P (2, 1)$ ，当线段 $A B$ 长最小时椭圆 $C$ 的离心率为．

查看试题解析
17. 已知 $O$ 是椭圆 $E$ 的对称中心， $F_{1} ， F_{2}$ 是 $E$ 的焦点.以 $O$ 为圆心， $O F_{1}$ 为半径的圆与 $E$ 的一个交点为 $A$ .若 $\vec{A F_{1}}$ 与 $\vec{A F_{2}}$ 的长度之比为2：1，则 $E$ 的离心率等于.

查看试题解析
18. 已知椭圆C $\frac{x^{2}}{a^{2}} + y^{2} = 1$ （a>1）的焦点为F₁、F₂ ，以原点为圆心、椭圆的焦距为直径的⊙O与椭圆C交于点P，则△PF₁F₂=.

查看试题解析
19. 焦点在x轴上，短轴长等于16，离心率等于 $\frac{3}{5}$ 的椭圆的标准方程为．

查看试题解析
20. 已知椭圆中心在原点，一个焦点为( $\sqrt{3}$ ，0)，且长轴长是短轴长的2倍，则该椭圆的标准方程是

查看试题解析

三、解答题

21. 已知中心在原点O，焦点在x轴的椭圆C的离心率为 $\frac{\sqrt{3}}{2}$ ，点A,B分别是椭圆C的长轴，短轴的端点，点O到直线AB的距离为 $\frac{6 \sqrt{5}}{5}$ .

(1)、求椭圆C的方程。

(2)、已知点 $E (3, 0)$ ,设点P,Q是椭圆C上的两动点，满足 $E P ⊥ E Q$ ,求 $\overset{⇀}{E P} \cdot \overset{⇀}{Q P}$ 的最小值。

查看试题解析
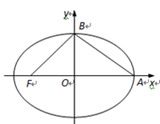22. 如图，在平面直角坐标系xOy中，椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > b > 0)$ 的左焦点为 $F$ ，右顶点为 $A$ ，上顶点为 $B$ ．

(1)、已知椭圆的离心率为 $\frac{1}{2}$ ，线段 $A F$ 中点的横坐标为 $\frac{\sqrt{2}}{2}$ ，求椭圆的标准方程；

(2)、已知△ $A B F$ 外接圆的圆心在直线 $y = - x$ 上，求椭圆的离心率 $e$ 的值．

查看试题解析
23. 在直角坐标系 $x O y$ 中，已知椭圆 $C : \frac{y^{2}}{a^{2}} + \frac{x^{2}}{b^{2}} = 1 (a > b > 0)$ 的上下两个焦点分别为 $F_{2}, F_{1}$ ，且 $| F_{1} F_{2} | = 2 \sqrt{2}$ ，椭圆过点 $(- 1, \sqrt{2})$ ．

(1)、求椭圆 $C$ 的标准方程；

(2)、设椭圆 $C$ 的一个顶点为 $B (b, 0)$ ，直线 $B F_{2}$ 交椭圆 $C$ 于另一个点 $N$ ，求 $Δ F_{1} B N$ 的面积．

查看试题解析
24. 设 $F_{1}, F_{2}$ 分别是椭圆 $E$ : $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > b > 0)$ 的左、右焦点，过 $F_{1}$ 作斜率为1的直线 $l$ 与椭圆 $E$ 相交于 $A, B$ 两点，且椭圆 $E$ 上存在点 $P$ ,使 $\overset{⇀}{O P} = \overset{⇀}{O A} + \overset{⇀}{O B}$ ( $O$ 为坐标原点).

(1)、求椭圆 $E$ 的离心率；

(2)、 $\overset{⇀}{O A} \cdot \overset{⇀}{O B} = - \frac{7}{4}$ ，求椭圆 $E$ 的方程.

查看试题解析

备考2020年高考数学一轮复习：49 椭 圆

一、单选题

二、填空题

三、解答题

备考2020年高考数学一轮复习：49 椭圆