备考2020年高考数学一轮复习:47 圆的方程
试卷更新日期:2019-11-01 类型:一轮复习
一、单选题
-
1. 一个圆经过以下三个点 , , ,且圆心在 轴上,则圆的标准方程为( )A、 B、 C、 D、2. 圆(x-3)2+(y+2)2=16的圆心坐标是( )A、(-3,2) B、(2,-3) C、(-2,3) D、(3,-2)3. 已知圆x2+y2+Dx+Ey+F=0的圆心坐标为(-2,3),半径为2,D,E分别为( )A、4,-6 B、-4,-6 C、-4,6 D、4,64. 圆心为 且过原点的圆的方程是( )A、 B、 C、 D、5. 圆 的圆心坐标和半径分别是( )A、 2 B、 4 C、 2 D、 46. 若方程 表示一个圆,则 的取值范围是( )A、 B、 C、 D、7. 若点P(1,-1)在圆C:x2+y2-x+y+m=0的外部,则实数m的取值范围是( )A、 B、 C、 D、8. 已知圆 为坐标原点,则以 为直径的圆的方程( )A、 B、 C、 D、9. 以A(-2,1),B(1,5)为半径两端点的圆的方程是( )A、(x+2)2+(y-1)2=25 B、(x-1)2+(y-5)2=25 C、(x+2)2+(y-1)2=25或(x-1)2+(y-5)2=25 D、(x+2)2+(y-1)2=5或(x-1)2+(y-5)2=510. 点P 在圆 的内部,则 的取值范围是 ( )A、
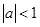 B、
B、 C、
C、 D、
D、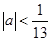 11. 圆 半径为 ,圆心在x轴的正半轴上,直线3x+4y+4=0与圆 相切,则圆 的方程为( )A、
11. 圆 半径为 ,圆心在x轴的正半轴上,直线3x+4y+4=0与圆 相切,则圆 的方程为( )A、 B、
B、 C、
C、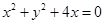 D、
D、 12. 方程 不能表示圆,则实数 的值为( )A、0 B、1 C、
12. 方程 不能表示圆,则实数 的值为( )A、0 B、1 C、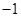 D、2
D、2
二、填空题
-
13. 公元前3世纪,古希腊数学家阿波罗尼斯在前人的基础上写了一部划时代的著作《圆锥曲线论》,该书给出了当时数学家们所研究的六大轨迹问题,其中之一便是“到两个定点的距离之比等于不为1的常数的轨迹是圆”,简称“阿氏圆”.用解析几何方法解决“到两个定点 , 的距离之比为 的动点 轨迹方程是: ”,则该“阿氏圆”的圆心坐标是 , 半径是 .14. 若方程x²+ +2x+4y+5k=0表示圆,则实数k的取值范围是。15. 已知两点 ,则以线段 为直径的圆的标准方程为 .16. 已知圆 经过点 , ,与直线 相切,则圆 的标准方程为 .17. 已知 , 分别是双曲线 : 的左、右顶点, 为 上一点,则 的外接圆的标准方程为 .18. 以古希腊数学家阿波罗尼斯命名的阿波罗尼斯圆,是指到两定点的距离之比为常数 的动点M的轨迹,若已知 , ,动点M满足 ,此时阿波罗尼斯圆的方程为 .
三、解答题