2016-2017学年吉林省长春108中七年级下学期期中数学试卷

试卷更新日期：2017-07-13 类型：期中考试

进入出卷网下载

一、选择题

1. 若一个数的平方根与它的立方根完全相同．则这个数是（）

A、1 B、﹣1 C、0 D、±1，0

查看试题解析
2. 如图，已知AB∥DE，∠ABC=80°，∠CDE=140°，则∠C=（）

A、20° B、30° C、40° D、50°

查看试题解析
3. 若a是（﹣3）²的平方根，则 $\sqrt[3]{a}$ 等于（）

A、﹣3 B、 $\sqrt[3]{3}$ C、 $\sqrt[3]{3}$ 或﹣ $\sqrt[3]{3}$ D、3或﹣3

查看试题解析
4. 在实数 $\sqrt[3]{- 27}$ ，3.1415926，0.123123123…，π² ， $\sqrt[3]{4}$ ， $\frac{10}{3}$ ， $\sqrt{25}$ ， $\frac{\sqrt{2}}{2}$ ，0.1010010001…（相邻两个1中间一次多1个0）中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 有下列命题：
①两条直线被第三条直线所截，同位角相等；
②0.1 的算术平方根是0.01；
③算术平方根等于它本身的数是1；
④如果点P（3﹣2n，1）到两坐标轴的距离相等，则n=1；
⑤若a²=b² ，则a=b；
⑥若 $\sqrt[3]{a}$ = $\sqrt[3]{b}$ ，则a=b．
其中假命题的个数是（）

A、3个 B、4 个 C、5个 D、6个

查看试题解析
6. 在平面直角坐标系内，线段CD是由线段AB平移得到的，点A（﹣2，3）的对应点为C（2，5），则点B（﹣4，﹣1）的对应点D的坐标为（）

A、（﹣8，﹣3） B、（4，2） C、（0，1） D、（1，8）

查看试题解析
7. 下列条件中不能判定AB∥CD的是（）

A、∠1=∠4 B、∠2=∠3 C、∠5=∠B D、∠BAD+∠D=180°

查看试题解析
8. 已知A（a，0）和B点（0，10）两点，且AB与坐标轴围成的三角形的面积等于20，则a的值为（）

A、2 B、4 C、0或4 D、4或﹣4

查看试题解析

二、填空题

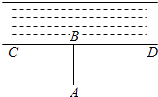
9. 点N（x，y）的坐标满足xy＜0，则点N在第象限．

查看试题解析
10. 如图，计划把河水引到水池A中，先作AB⊥CD，垂足为B，然后沿AB开渠，能使所开的渠道最短，这样设计的依据是

查看试题解析
11. 已知 $\sqrt{x + 3}$ +|3x+2y﹣15|=0，则 $\sqrt{x + y}$ 的算术平方根为．

查看试题解析
12. 如图，O对应的有序数对为（1，3）有一个英文单词的字母顺序对应如图中的有序数对分别为（1，2），（5，1），（5，2），（5，2），（1，3），请你把这个英文单词写出来或者翻译成中文为．

查看试题解析
13. 已知∠AOB与∠BOC互为邻补角，且∠BOC＞∠AOB．OD平分∠AOB，射线OE使∠BOE= $\frac{1}{2}$ ∠EOC，当∠DOE=72°时，则∠EOC的度数为．

查看试题解析
14. 如图，把一张长方形纸片ABCD沿EF折叠后，D、C分别在M、N的位置上，EM与BC的交点为G，若∠EFG=65°，则∠2= ．

查看试题解析
15. 在数轴上﹣ $\sqrt{2}$ 与﹣2之间的距离为．

查看试题解析
16. 观察下列各式： $\sqrt{1 + \frac{1}{3}} = 2 \sqrt{\frac{1}{3}} ， \sqrt{2 + \frac{1}{4}} = 3 \sqrt{\frac{1}{4}} ， \sqrt{3 + \frac{1}{5}} = 4 \sqrt{\frac{1}{5}}$ ，…，根据你发现的规律，若式子 $\sqrt{a + \frac{1}{b}} = 8 \sqrt{\frac{1}{b}}$ （a、b为正整数）符合以上规律，则 $\sqrt{a + b}$ = ．

查看试题解析

三、解答题

17. 将下列各数填入相应的集合内．
﹣7，0.32， $\frac{1}{3}$ ，0， $\sqrt{8}$ ， $\sqrt{\frac{1}{2}}$ ， $\sqrt[3]{125}$ ，π，0.1010010001…
①有理数集合
②无理数集合
③负实数集合

查看试题解析
18. 根据要求计算：

(1)、计算：| $\sqrt{2}$ ﹣ $\sqrt{3}$ |+ $\sqrt[3]{8}$ + $\sqrt{{(- 2)}^{2}}$

(2)、解方程组：
① ${\begin{matrix} 4 x - 3 y = 11 \\ 2 x + y = 13 \end{matrix}$
② ${\begin{matrix} 4 (x - y - 1) = 3 (1 - y) - 2 \\ \frac{x}{2} + \frac{y}{3} = 2 \end{matrix}$ ．

查看试题解析
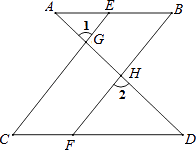
19. 完成下面推理过程：
如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．理由如下：
∵∠1=∠2（已知），
且∠1=∠CGD（），
∴∠2=∠CGD（等量代换）．
∴CE∥BF（）．
∴∠ =∠C（）．
又∵∠B=∠C（已知），
∴∠ =∠B（等量代换）．
∴AB∥CD（）．

查看试题解析
20. 若 $\sqrt{13}$ 的整数部分为a，小数部分为b，求a²+b﹣ $\sqrt{13}$ 的值．

查看试题解析
21. 李大叔去年承包了10亩地种植甲、乙两种蔬菜，共获利18000元，其中甲种蔬菜每亩获利2000元，乙种蔬菜每亩获利1500元，李大叔去年甲、乙两种蔬菜各种植了多少亩？

查看试题解析
22. 如图，△ABC在直角坐标系中

(1)、若把△ABC向上平移2个单位，再向左平移1个单位得到△A′B′C′，写出 A′、B′、C′的坐标，并在图中画出平移后图形．

(2)、求出三角形ABC的面积．

查看试题解析
23. MF⊥NF于F，MF交AB于点E，NF交CD于点G，∠1=140°，∠2=50°，试判断AB和CD的位置关系，并说明理由．

查看试题解析
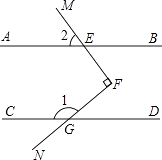24. 如图，已知∠1，∠2互为补角，且∠3=∠B，

(1)、求证：∠AFE=∠ACB；

(2)、若CE平分∠ACB，且∠1=80°，∠3=45°，求∠AFE的度数．

查看试题解析

四、附加题

25. 如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°

(1)、请判断AB与CD的位置关系并说明理由；

(2)、如图2，在（1）的结论下，当∠E=90°保持不变，移动直角顶点E，使∠MCE=∠ECD，当直角顶点E点移动时，问∠BAE与∠MCD是否存在确定的数量关系？

(3)、如图3，在（1）的结论下，P为线段AC上一定点，点Q为直线CD上一动点，当点Q在射线CD上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？
（2、3小题只需选一题说明理由）

查看试题解析