2017年贵州省六盘水市中考数学试卷
试卷更新日期:2017-07-12 类型:中考真卷
一、选择题:
-
1. 大米包装袋上(10±0.1)kg的标识表示此袋大米重( )A、(9.9~10.1)kg B、10.1kg C、9.9kg D、10kg2. 国产越野车“BJ40”中,哪个数字或字母既是中心对称图形又是轴对称图形( )A、B B、J C、4 D、03. 下列式子正确的是( )A、7m+8n=8m+7n B、7m+8n=15mn C、7m+8n=8n+7m D、7m+8n=56mn4. 如图,梯形ABCD中,AB∥CD,∠D=( )
 A、120° B、135° C、145° D、155°5. 已知A组四人的成绩分别为90、60、90、60,B组四人的成绩分别为70、80、80、70,用下列哪个统计知识分析区别两组成绩更恰当( )A、平均数 B、中位数 C、众数 D、方差6. 不等式3x+6≥9的解集在数轴上表示正确的是( )A、
A、120° B、135° C、145° D、155°5. 已知A组四人的成绩分别为90、60、90、60,B组四人的成绩分别为70、80、80、70,用下列哪个统计知识分析区别两组成绩更恰当( )A、平均数 B、中位数 C、众数 D、方差6. 不等式3x+6≥9的解集在数轴上表示正确的是( )A、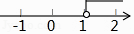 B、
B、 C、
C、 D、
D、 7. 国产大飞机C919用数学建模的方法预测的价格是(单位:美元):5098,5099,5001,5002,4990,4920,5080,5010,4901,4902,这组数据的平均数是( )A、5000.3 B、4999.7 C、4997 D、50038. 使函数y= 有意义的自变量x的取值范围是( )A、x≥3 B、x≥0 C、x≤3 D、x≤09. 已知二次函数y=ax2+bx+c的图象如图所示,则( )
7. 国产大飞机C919用数学建模的方法预测的价格是(单位:美元):5098,5099,5001,5002,4990,4920,5080,5010,4901,4902,这组数据的平均数是( )A、5000.3 B、4999.7 C、4997 D、50038. 使函数y= 有意义的自变量x的取值范围是( )A、x≥3 B、x≥0 C、x≤3 D、x≤09. 已知二次函数y=ax2+bx+c的图象如图所示,则( ) A、b>0,c>0 B、b>0,c<0 C、b<0,c<0 D、b<0,c>010. 矩形的两边长分别为a、b,下列数据能构成黄金矩形的是( )A、a=4,b= +2 B、a=4,b= ﹣2 C、a=2,b= +1 D、a=2,b= ﹣111. 桌面上放置的几何体中,主视图与左视图可能不同的是( )A、圆柱 B、正方体 C、球 D、直立圆锥12. 三角形的两边a、b的夹角为60°且满足方程x2﹣3 x+4=0,则第三边的长是( )
A、b>0,c>0 B、b>0,c<0 C、b<0,c<0 D、b<0,c>010. 矩形的两边长分别为a、b,下列数据能构成黄金矩形的是( )A、a=4,b= +2 B、a=4,b= ﹣2 C、a=2,b= +1 D、a=2,b= ﹣111. 桌面上放置的几何体中,主视图与左视图可能不同的是( )A、圆柱 B、正方体 C、球 D、直立圆锥12. 三角形的两边a、b的夹角为60°且满足方程x2﹣3 x+4=0,则第三边的长是( )
A、 B、2 C、2 D、3二、填空题
-
13. 中国“蛟龙号”深潜器下潜深度为7062米,用科学记数法表示为米.14. 计算:2017×1983= .15. 定义:A={b,c,a},B={c},A∪B={a,b,c},若M={﹣1},N={0,1,﹣1},则M∪N={}.16. 如图,在正方形ABCD中,等边三角形AEF的顶点E、F分别在边BC和CD上,则∠AEB=度.
 17. 方程 ﹣ =1的解为x= .18. 如图,在▱ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF= .
17. 方程 ﹣ =1的解为x= .18. 如图,在▱ABCD中,对角线AC、BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF= . 19. 已知A(﹣2,1),B(﹣6,0),若白棋A飞挂后,黑棋C尖顶,黑棋C的坐标为().
19. 已知A(﹣2,1),B(﹣6,0),若白棋A飞挂后,黑棋C尖顶,黑棋C的坐标为(). 20. 计算1+4+9+16+25+…的前29项的和是 .
20. 计算1+4+9+16+25+…的前29项的和是 .
三、解答题
-
21. 计算:(1)、2﹣1+sin30°﹣|﹣2|;(2)、(﹣1)0﹣|3﹣π|+ .22. 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.
 (1)、画出△ABC关于原点成中心对称的△A'B'C',并直接写出△A'B'C'各顶点的坐标.(2)、求点B旋转到点B'的路径长(结果保留π).23. 端午节当天,小明带了四个粽子(除味道不同外,其它均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.(1)、请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性.(2)、请你计算小红拿到的两个粽子刚好是同一味道的概率.24. 甲乙两个施工队在六安(六盘水﹣安顺)城际高铁施工中,每天甲队比乙队多铺设100米钢轨,甲队铺设5天的距离刚好等于乙队铺设6天的距离.若设甲队每天铺设x米,乙队每天铺设y米.(1)、依题意列出二元一次方程组;(2)、求出甲乙两施工队每天各铺设多少米?
(1)、画出△ABC关于原点成中心对称的△A'B'C',并直接写出△A'B'C'各顶点的坐标.(2)、求点B旋转到点B'的路径长(结果保留π).23. 端午节当天,小明带了四个粽子(除味道不同外,其它均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.(1)、请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性.(2)、请你计算小红拿到的两个粽子刚好是同一味道的概率.24. 甲乙两个施工队在六安(六盘水﹣安顺)城际高铁施工中,每天甲队比乙队多铺设100米钢轨,甲队铺设5天的距离刚好等于乙队铺设6天的距离.若设甲队每天铺设x米,乙队每天铺设y米.(1)、依题意列出二元一次方程组;(2)、求出甲乙两施工队每天各铺设多少米?