2017年北京市中考数学试卷
试卷更新日期:2017-07-12 类型:中考真卷
一、选择题
-
1. 如图所示,点P到直线l的距离是( )
 A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段PD的长度2. 若代数式 有意义,则实数x的取值范围是( )A、x=0 B、x=4 C、x≠0 D、x≠43. 如图是某个几何体的展开图,该几何体是( )
A、线段PA的长度 B、线段PB的长度 C、线段PC的长度 D、线段PD的长度2. 若代数式 有意义,则实数x的取值范围是( )A、x=0 B、x=4 C、x≠0 D、x≠43. 如图是某个几何体的展开图,该几何体是( )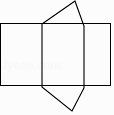 A、三棱柱 B、圆锥 C、四棱柱 D、圆柱4. 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
A、三棱柱 B、圆锥 C、四棱柱 D、圆柱4. 实数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )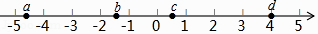 A、a>﹣4 B、bd>0 C、|a|>|d| D、b+c>05. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、
A、a>﹣4 B、bd>0 C、|a|>|d| D、b+c>05. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、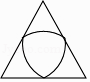 B、
B、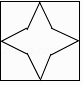 C、
C、 D、
D、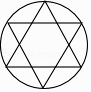 6. 若正多边形的一个内角是150°,则该正多边形的边数是( )A、6 B、12 C、16 D、187. 如果a2+2a﹣1=0,那么代数式(a﹣ )• 的值是( )A、﹣3 B、﹣1 C、1 D、38. 下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况.
6. 若正多边形的一个内角是150°,则该正多边形的边数是( )A、6 B、12 C、16 D、187. 如果a2+2a﹣1=0,那么代数式(a﹣ )• 的值是( )A、﹣3 B、﹣1 C、1 D、38. 下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况.2011﹣2016年我国与东南亚地区和东欧地区的贸易额统计图

(以上数据摘自《“一带一路”贸易合作大数据报告(2017)》)
根据统计图提供的信息,下列推理不合理的是( )
A、与2015年相比,2016年我国与东欧地区的贸易额有所增长 B、2011﹣2016年,我国与东南亚地区的贸易额逐年增长 C、2011﹣2016年,我国与东南亚地区的贸易额的平均值超过4200亿美元 D、2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多9. 小苏和小林在如图1所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图2所示.下列叙述正确的是( ) A、两人从起跑线同时出发,同时到达终点 B、小苏跑全程的平均速度大于小林跑全程的平均速度 C、小苏前15s跑过的路程大于小林前15s跑过的路程 D、小林在跑最后100m的过程中,与小苏相遇2次10. 如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.
A、两人从起跑线同时出发,同时到达终点 B、小苏跑全程的平均速度大于小林跑全程的平均速度 C、小苏前15s跑过的路程大于小林前15s跑过的路程 D、小林在跑最后100m的过程中,与小苏相遇2次10. 如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.
下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A、① B、② C、①② D、①③二、填空题
-
11. 写出一个比3大且比4小的无理数: .12. 某活动小组购买了4个篮球和5个足球,一共花费了435元,其中篮球的单价比足球的单价多3元,求篮球的单价和足球的单价.设篮球的单价为x元,足球的单价为y元,依题意,可列方程组为 .13. 如图,在△ABC中,M、N分别为AC,BC的中点.若S△CMN=1,则S四边形ABNM= .
 14. 如图,AB为⊙O的直径,C、D为⊙O上的点,AD=CD.若∠CAB=40°,则∠CAD= .
14. 如图,AB为⊙O的直径,C、D为⊙O上的点,AD=CD.若∠CAB=40°,则∠CAD= . 15. 如图,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一中由△OCD得到△AOB的过程: .
15. 如图,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一中由△OCD得到△AOB的过程: . 16.
16.图1是“作已知直角三角形的外接圆”的尺规作图过程
已知:Rt△ABC,∠C=90°,求作Rt△ABC的外接圆.
作法:如图2.
 (1)、①分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于P,Q两点;
(1)、①分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于P,Q两点;②作直线PQ,交AB于点O;
(2)、以O为圆心,OA为半径作⊙O.⊙O即为所求作的圆.请回答:该尺规作图的依据是 .
三、解答题
-
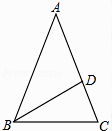
17. 计算:4cos30°+(1﹣ )0﹣ +|﹣2|.18. 解不等式组: .19. 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D.
求证:AD=BC.
 20. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
20. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.(以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》)
请根据该图完成这个推论的证明过程.

证明:S矩形NFGD=S△ADC﹣(S△ANF+S△FGC),S矩形EBMF=S△ABC﹣(+).
易知,S△ADC=S△ABC , = , = .
可得S矩形NFGD=S矩形EBMF .
21. 关于x的一元二次方程x2﹣(k+3)x+2k+2=0.(1)、求证:方程总有两个实数根;(2)、若方程有一根小于1,求k的取值范围.22. 如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.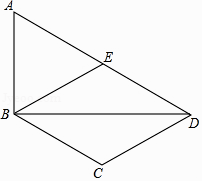 (1)、求证:四边形BCDE为菱形;(2)、连接AC,若AC平分∠BAD,BC=1,求AC的长.23. 如图,在平面直角坐标系xOy中,函数y= (x>0)的图象与直线y=x﹣2交于点A(3,m).
(1)、求证:四边形BCDE为菱形;(2)、连接AC,若AC平分∠BAD,BC=1,求AC的长.23. 如图,在平面直角坐标系xOy中,函数y= (x>0)的图象与直线y=x﹣2交于点A(3,m). (1)、求k、m的值;(2)、已知点P(n,n)(n>0),过点P作平行于x轴的直线,交直线y=x﹣2于点M,过点P作平行于y轴的直线,交函数y= (x>0)的图象于点N.
(1)、求k、m的值;(2)、已知点P(n,n)(n>0),过点P作平行于x轴的直线,交直线y=x﹣2于点M,过点P作平行于y轴的直线,交函数y= (x>0)的图象于点N.①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.
24. 如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D. (1)、求证:DB=DE;(2)、若AB=12,BD=5,求⊙O的半径.25. 某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
(1)、求证:DB=DE;(2)、若AB=12,BD=5,求⊙O的半径.25. 某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩x
人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
(说明:成绩80分及以上为生产技能优秀,70﹣﹣79分为生产技能良好,60﹣﹣69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门
平均数
中位数
众数
甲
78.3
77.5
75
乙
78
80.5
81
得出结论:a.估计乙部门生产技能优秀的员工人数为;b.可以推断出部门员工的生产技能水平较高,理由为 . (至少从两个不同的角度说明推断的合理性)
26. 如图,P是AB所对弦AB上一动点,过点P作PM⊥AB交AB于点M,连接MB,过点P作PN⊥MB于点N.已知AB=6cm,设A、P两点间的距离为xcm,P、N两点间的距离为ycm.(当点P与点A或点B重合时,y的值为0)
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东的探究过程,请补充完整:
(1)、通过取点、画图、测量,得到了x与y的几组值,如下表:x/cm
0
1
2
3
4
5
6
y/cm
0
2.0
2.3
2.1
0.9
0
(说明:补全表格时相关数值保留一位小数)
(2)、建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象. (3)、结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为cm.27. 在平面直角坐标系xOy中,抛物线y=x2﹣4x+3与x轴交于点A、B(点A在点B的左侧),与y轴交于点C.(1)、求直线BC的表达式;(2)、垂直于y轴的直线l与抛物线交于点P(x1 , y1),Q(x2 , y2),与直线BC交于点N(x3 , y3),若x1<x2<x3 , 结合函数的图象,求x1+x2+x3的取值范围.28. 在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.
(3)、结合画出的函数图象,解决问题:当△PAN为等腰三角形时,AP的长度约为cm.27. 在平面直角坐标系xOy中,抛物线y=x2﹣4x+3与x轴交于点A、B(点A在点B的左侧),与y轴交于点C.(1)、求直线BC的表达式;(2)、垂直于y轴的直线l与抛物线交于点P(x1 , y1),Q(x2 , y2),与直线BC交于点N(x3 , y3),若x1<x2<x3 , 结合函数的图象,求x1+x2+x3的取值范围.28. 在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M. (1)、若∠PAC=α,求∠AMQ的大小(用含α的式子表示).(2)、用等式表示线段MB与PQ之间的数量关系,并证明.29. 在平面直角坐标系xOy中的点P和图形M,给出如下的定义:若在图形M上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为图形M的关联点.
(1)、若∠PAC=α,求∠AMQ的大小(用含α的式子表示).(2)、用等式表示线段MB与PQ之间的数量关系,并证明.29. 在平面直角坐标系xOy中的点P和图形M,给出如下的定义:若在图形M上存在一点Q,使得P、Q两点间的距离小于或等于1,则称P为图形M的关联点.
(1)、当⊙O的半径为2时,①在点P1( ,0),P2( , ),P3( ,0)中,⊙O的关联点是 .
②点P在直线y=﹣x上,若P为⊙O的关联点,求点P的横坐标的取值范围.
(2)、⊙C的圆心在x轴上,半径为2,直线y=﹣x+1与x轴、y轴交于点A、B.若线段AB上的所有点都是⊙C的关联点,直接写出圆心C的横坐标的取值范围.